Web Lesson 14: Transformations 2
The Interactive Web-Lesson below has questions embedded
So do it carefully, as your answers are sent to me!
- When a question pops up, if you want to see the movie again, click Hide (top right corner)
- You CAN'T retry a flopped question: So PAY ATTENTION and THINK!
- When you get a question CORRECT, you'll get an opportunity to SKIP the explanation:
Click the arrow in the right (but be quick!)
Sketching Curves using Transformations
Rules 1-6 we already knew from Web Lesson #13
Rule 1: Make sure the brackets are shown. Fractions often have brackets that we don't bother to show:
y = 1 should be written: y = 1
x-2 (x-2)
y = 4 - sin x can be written as: y = 4 - sin(x)
Rule 2:
The term with 'x' in it should be the first term. If not, then swap the terms:
y = 4 - x³ can be written as: y = - x³ + 4
└─┘└─────┘ └────┘└────┘
Rule 3: +k INSIDE the brackets shifts the curve left by k
Rule 4: A +C OUTSIDE the brackets shifts the curve up by +C
Rule 5: A (i.e. a negative sign, or a Χ-1) OUTSIDE the brackets reflects the curve in the x-axis
Rule 6:A (i.e. a negative sign, or a Χ-1) INSIDE the brackets reflects the curve in the y-axis
The NEW RULES we are ADDING today are:
Rule 7:
A ΧB INSIDE the brackets squashes the curve by B along x (a squash of \(\times B\) is the same as a stretch of \(\times \frac{1}{B}\))
Rule 8:
A ΧA OUTSIDE the brackets stretches the curve by A along y
Note:
A stretch of 1/3 is the same as a squash of 3
A squash of 1/4 is the same as a stretch of 4
A stretch of 1/5 is the same as a squash of 5
╘═════════╤═════════╛ ╘══════════╤══════╛
│ │
│ ┌─────────────────────────────────┐ │
└───►┤ It's easier to perform the ├►───┘
│ transformation when written │
│ so the number describing the │
│ stretch/squash is bigger than 1 │
└─────────────────────────────────┘
The Cosine Curve:
Below is a graph of the \(y=\cos x\) curve (also called the "Cosine Curve"):
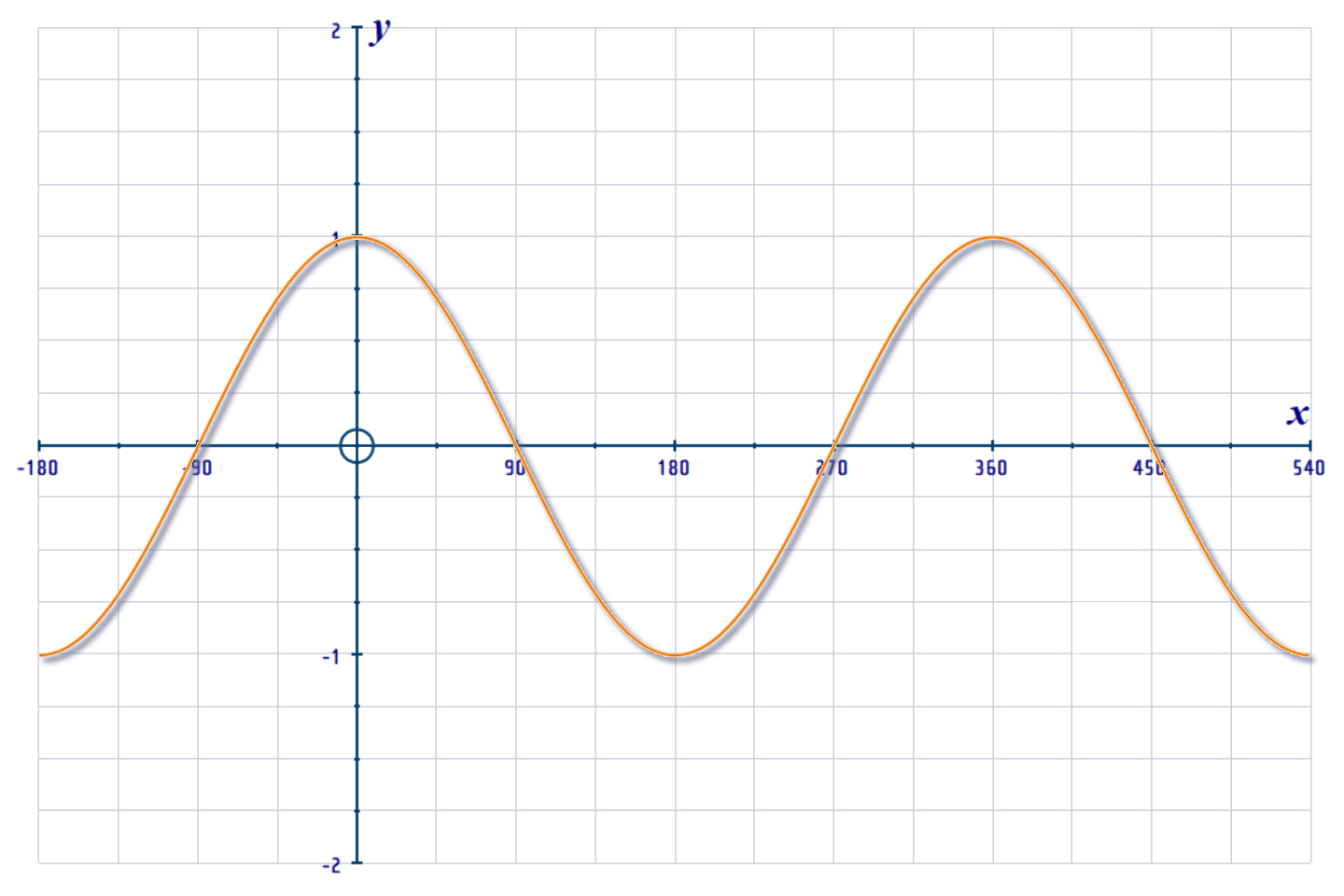
When performing transformations - it is best to start with 1-cycle of the (y=\cos x\) graph:
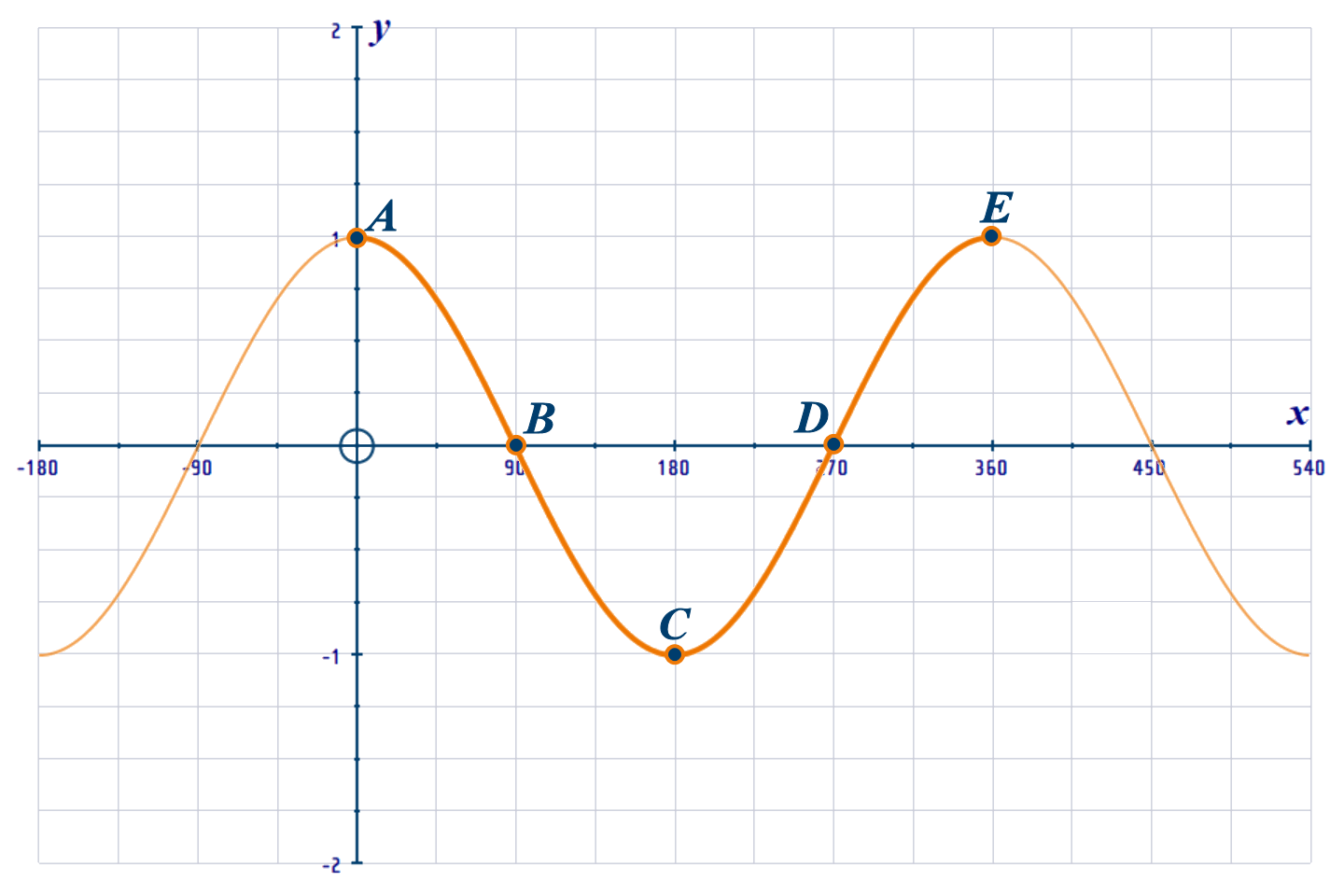
Starting with 1-cycle of \(y=\cos x\) (as shown above) and by using the same methods as in the movie, sketch the following curves. Use squared or graph paper and use a different grid for each curve.
Make sure you label the points, A, B, C, D and E on the transformed curve:
For each question, you must also state clearly the transformations you have made
Question 1: The PERIOD of any curve is the length (along the x-axis) of 1-complete cycle of the curve
Sketch \(y\,=\,\cos \left( 3x \right) \) and hence determine the PERIOD of the curve \(y=\cos \left( 3x \right) \)
Deduce the period of i) \(y=\cos \left( \frac{3}{4}x \right) \) ii) \(y=\cos \left( \frac{2}{5}x \right) \)
Clues:
There's only 1-transformation:
y = cos(3x)
▲ ┌─────────────────────────────────┐
└───────────────────┤ The Χ3 is inside the brackets │
│ so squash curve by 3 along x │
└─────────────────────────────────┘
But; a squash of 3 is the same as a stretch of ⅓
╘══════╤══════╛ ╘══════╤═══════╛
│ │
│ ┌─────────────────────────┐ │
└─►┤ It is easier to perform ├►─┤
│ the transformation when │ │
│ written like this │ │
└─────────────────────────┘ │
│
┌─────────────────┴─────────────────────────┐
│ NOT SURE how to stretch by 1/3 along x? │
├───────────────────────────────────────────┤
│ Pick some points on the curve (A,B,C,D,E
)│
│ Since we are stretching by 1/3 along x│
│ multiply all of the x-coordinates by 1/3│
└───────────────────────────────────────────┘
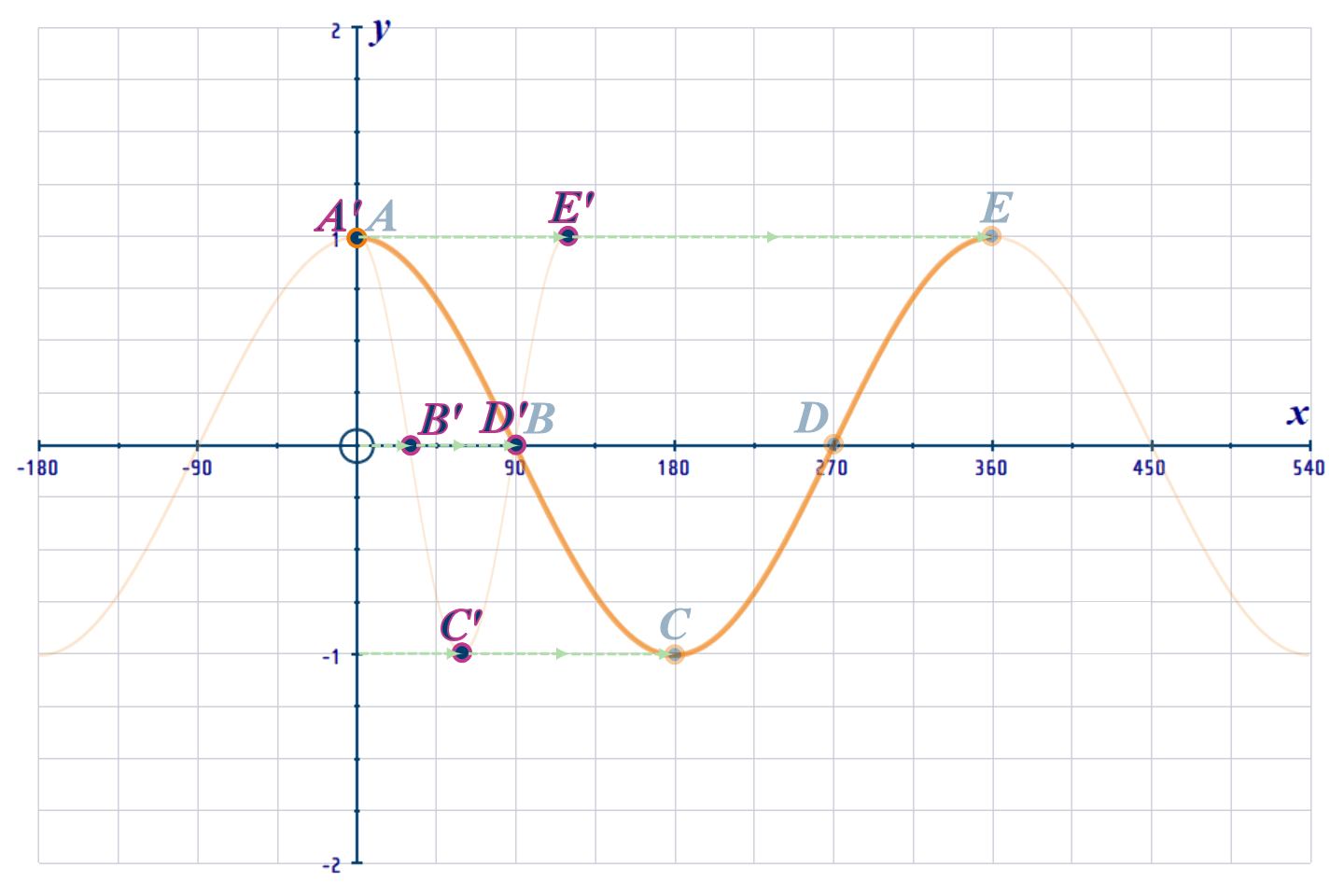
Note: It is easy to see the PERIOD as that's basically the x-coordinate of the last point
of our 1-cycle curve
The FREQUENCY is the number of cycles that will fit into 360°
There's a simple connection between PERIOD and FREQUENCY
┌──────────────┐ R-E-C-I-P ┌─────────────┐
│ PERIOD ╞════════════════════►│ FREQUENCY │
├──────────────┤ ├─────────────┤
│length of one │◄════════════════════╡ № of cycles │
│complete cycle│ R-E-C-I-P │ in 360° │
└──────────────┘ └─────────────┘
Question 2: Sketch: \(y\,=\,2\, -\,2\cos x\)
Clue:
┌───────────────────┐ ┌────────────────────┐
The method shown in the ANIMATION talks about: │INSIDE THE BRACKETS│ and │OUTSIDE THE BRACKETS│
└─────────┬─────────┘ └─────────┬──────────┘
┌─────────┴─────────┐ ┌─────────┴──────────┐
In these hints, we'll use a FLOW-DIAGRAM & say:│BEFORE THE FUNCTION│ and │ AFTER THE FUNCTION │
└───────────────────┘ └────────────────────┘
three→operations→outside →
←nothing←much ╔═══════════════════════════╗↓
↓┌─────────────║────────┐ ║t
i│ ┌───╨───┐ ┌┴┐ ║h
n│ y = 2 ─ 2 cos(x) ║e → b→r→a→c→k→e→t→s→!
s│ ▲ ▲ ▲ ╔═══════════╧══════════════════════╗
i│ └──│──│────────────║───────────────────────────────┐ ║
d│ brackets └──│────────────║─────────────────┐ │ ║
e│the┌───────┐ └────────────║───┐ │ │ ║
└───┘ ┌───┴───┐ ║ ┌┴─┐ ┌─┴─┐ ┌─┴┐ ║
x ─────────► COS ───────║─►│Χ2│────────►│Χ-1│────────►│+2│ ║
└─┬─┘ ║ └┬─┘ └─┬─┘ └─┬┘ ║
f(x) ╚═══│═════════════│═════════════│══╝
┌───────────┴───┐ │ │
│ Χ2 after f(x) │ │ │
│ stretch by 2│ │ │
│ parallel to y │ │ └──────────┐
└───────────┬───┘┌────────┴──────────┐ │
│ │Χ-1 is after f(x)│ │
│ │ REFLECT IN x-AXIS │┌────────────┴──────┐
│ └───────────────────┘│ +2 is after f(x)│
│ │TRANSLATE ? along y│
│ └───────────────────┘
│
│
┌────────────────────────────────┴──────────┐
│ Not sure how to stretch by 2? Here's HOW: └───────────────┐
│ Pick a few points along the curve (i.e. A, B, C, D & E): └─────────────────────┐
│ Since we are stretching by 2 along y, multiply all of the y-coordinates by 2│
└─────────────────────────────────────────────────────────────────────────────────┘
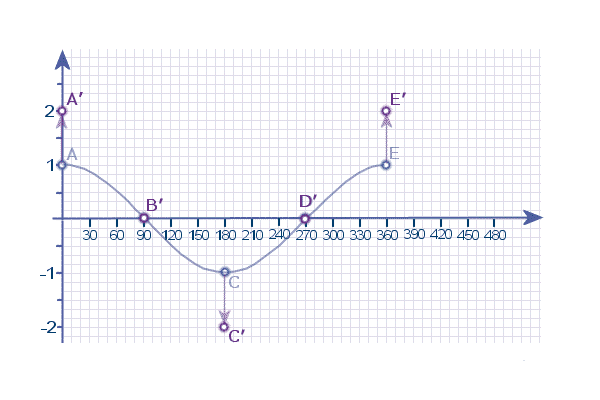
And connect these points up again to form the stretched curve:
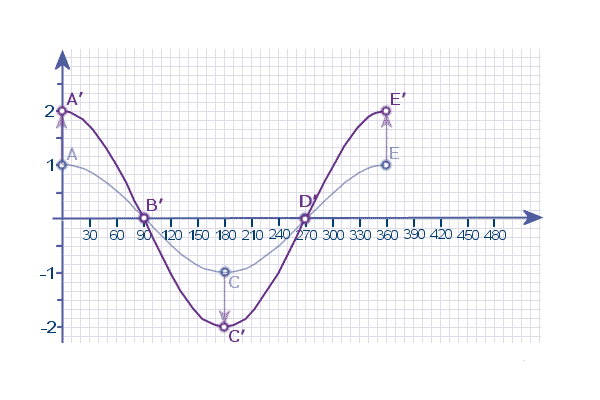
(Notice that B and D didn't move - because their y-coordinates were ZERO)
The remaining transformations - REFLECT in x and TRANSLATE BY 2 along the y-axis are easy
(you did stuff like that in Web Lesson 13)!
Question 3: Sketch: \(y\,=\,-1\,+\,2\cos \left( x\,-\,30 \right) \)
Clue:
Let's start by re-writing with the x term on the left:
y = -1 + 2 cos(x-30)
┌───────────────────┐ ┌────────────────────┐
The method shown in the Web Lesson talks about:│INSIDE THE BRACKETS│ and │OUTSIDE THE BRACKETS│
└─────────┬─────────┘ └─────────┬──────────┘
┌─────────┴─────────┐ ┌─────────┴──────────┐
In these hints, we use a FLOW-DIAGRAM and say: │BEFORE THE FUNCTION│ and │ AFTER THE FUNCTION │
└───────────────────┘ └────────────────────┘
Of course, these are essentially the same thing:
before f(x) f(x) after f(x)
┌──────┴──────┐ ┌─┴─┐ ┌───────────┴───────────┐
x ────│───► -30 ───│─────► COS ───│────► Χ2 ────────► -1 │
└──────┬──────┘ └─┬─┘ └───────────┬───────────┘
INSIDE BRACKETS │ OUTSIDE BRACKETS
└───────────────│────┐ │
┌────│────│────────────┘
┌───┴──┐┌┴┐┌──┴─┐
y = -1 + 2 cos(x-30)
▲ ▲ ▲ ┌─────────────────────────────┐
│ │ └────────────┤-30 is inside the brackets:│
▲ ▲ │so shifts curve LEFT by -30│
│ │ │ (i.e. same as:
by
) │
▲ ▲ └─────────────────────────────┘
│ │
▲ ▲ ┌─────────────────────────────┐
│ └────┤Χ2 is outside the brackets:│
▲ │so stretches the curve by 2│
│ │parallel to the y-axis┌──────┘
┌────────┴─────┐ └──────────────────────┘
BLAH BLAH BLAH
Question 4: Sketch: \(y\,=\,-3\cos \left( \frac{2}{3}x \right) \)
Clues:
Starting with a sketch of y = cos x:
y = -3cos(⅔x)
▲ ┌─────────────────────────────────┐
└───────────────────┤ The Χ2/3 is inside the brackets │
│ so squashes the curve by 2/3 │
│ along x │
└─────────────────────────────────┘
But; a squash of 2/3 is the same as a stretch of 3/2 (= 1.5)
╘═══════╤═══════╛ ╘════════╤══════════════╛
│ │
│ ┌─────────────────────────┐ │
└──►┤ It is easier to perform ├►──┤
│ the transformation when │ │
│ written like this │ │
└─────────────────────────┘ │
│
┌─────────────────┴─────────────────────────┐
│ NOT SURE how to stretch by 1.5 along x? │
├───────────────────────────────────────────┤
│ Pick some points on the curve (A,B,C,D,E
)│
│ Since we are stretching by 1.5 along x│
│ multiply all of the x-coordinates by 1.5│
└───────────────────────────────────────────┘
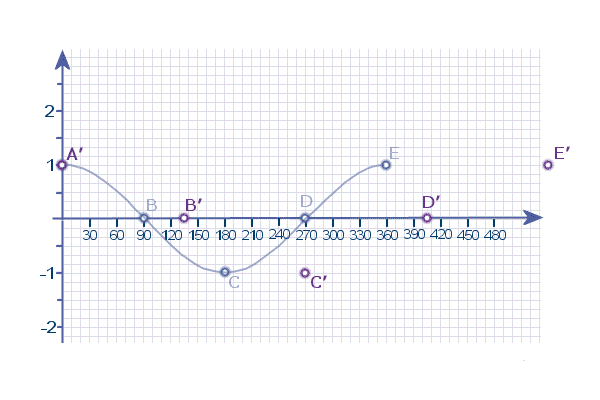
(Notice A didn't move - because its x-coordinate was ZERO)
And connect these points up again to form the stretched curve
Then carry on with the rest of the transformations
Question 5: Sketch: \(y\,=\,1\,+\,\cos \left( 90\,-\,2x \right) \)
Clues:
This is bit tricky - because these a lot of crap INSIDE THE BRACKETS
Remember the SOLUTION to the "MULTIPLE TRANSFORMATIONS INSIDE THE BRACKETS" problem?
┌──────┐
x ────────► Χ2 ────────► Χ-1 ─────────► +90 ────────► │ f(x) │ ────────► + 1
╘═══════════════╤═══════════════╛ └──────┘
│
┌────────────────┴─────────────────┐
┌─┘ You can see that there are THREE └─┐
│ transformations INSIDE the brackets! │
└──────────────────┬───────────────────┘
│
But we know, the SOLUTION IS SIMP│E; REVERSE the order of the operations INSIDE THE BRACKETS:
│
┌─────────┴───────┐ ┌──────┐
x ────────► Χ2 ────────► Χ-1 ─────────► +90 ────────► │ f(x) │ ────────► + 1
╘═╤═╛ ╘═╤═╛ ╘═╤═╛ └──────┘ ╘═╤═╛
│ │ ① │
│ │ │
│ ② │
│ │
③ │
│
④
It's still gonna be tricky, so here's an applet for you to check!
An unknown function:
Below is a graph of \(y=f\left( x \right) \):
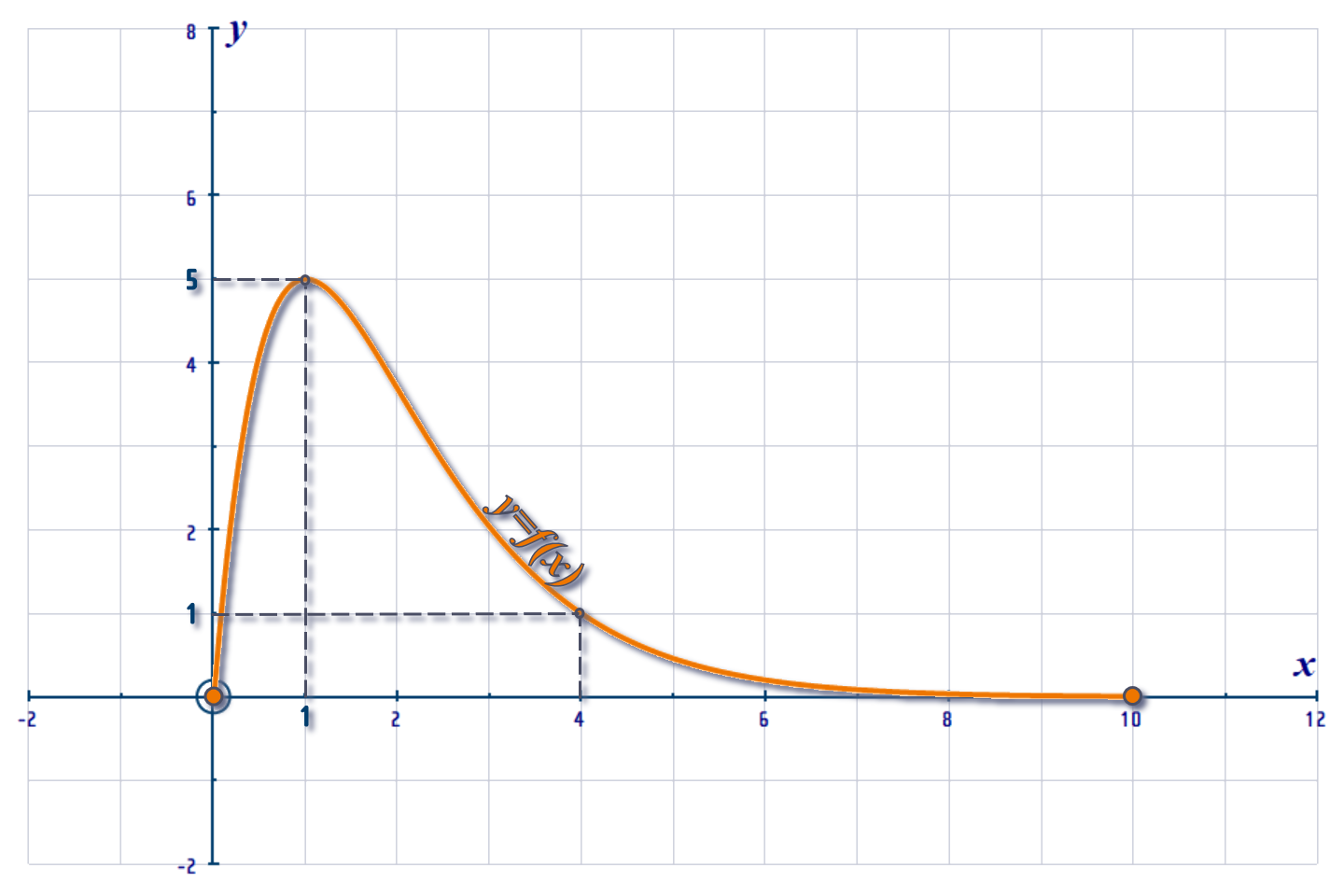
We are NOT told its equation: But we do know that \(f\left( x \right) \) is defined for \(0\leqslant x\leqslant 10\) and it has a root at \(x\,=\,0\) and another root at \(x\,=\,10\). The maximum point \(P\) is at \(\left( 1,5 \right) \).
It passes through the point \(Q\,=\,\left( 4, 1\right) \) and its gradient at \(Q\) is \(-\frac{3}{4}\)
The RANGE of \(y=f\left( x \right) \) is: \(0\leqslant yx\leqslant 5\)
Armed with this information about \(f\left( x \right) \) and the curve of \(y=f\left( x \right) \) (as shown above) and by using the same methods as in the movie, sketch the following curves.
Use squared or graph paper and use a different grid for each curve:
For each question, you must:
- State clearly the transformations you have made
- State the domain for which the transformed curve should be defined. Also state its range
- Identify the point \(P'\) (where \(P\,=\,\left( 1,5 \right) \) is on the transformed curve); and if \(P'\) is a maximum point
- Identify \(Q'\) (where \(Q\,=\,\left( 4,1 \right) \) is on the transformed curve); and state the gradient at \(Q'\)
- Identify where the points \(\left( 0,0 \right) \) and \(\left( 10,0 \right) \) have moved to; and determine if they are STILL roots
- Do you know the roots or the y-intercept of the transformed curve?
Question 6: Sketch: \(y\,=\,\frac{1}{2}f\left( \frac{1}{2}x \right) \)
Clue: ┌────────────────────────────┐
┌───────┤Χ½ is inside the brackets │
▼ │ so stretch by
along x │
y = ½f(½x) └────────────────────────────┘
▲ ┌──────────────────────────┐
└─────────────────────────────────┤Χ½ outside the brackets │
│ so stretch by
along y │
└──────────────────────────┘
A stretch of ... is the same as a squash of ...
So, to squash by ... along y, pick some points and divide the y-coordinates by ...
Question 7: Sketch: \(y\,=\,5 -\,f\left( \frac{2}{3}x \right) \)
Clue:
There are no brackets, so we put a brackets around the x:
y = f(⅔x)
▲ ┌──────────────────────────────┐
└────────────────────────┤ The Χ⅔ is inside the brackets│
│ so squashes the curve by ⅔ │
│ along y │
└──────────────────────────────┘
But; a squash of 2/3 is the same as a stretch of 3/2
╘═══════╤═══════╛ ╘════════╤═══════╛
│ │
│ ┌─────────────────────────┐ │
└──►┤ It is easier to perform ├►──┘
│ the transformation when │
│ written like this │
└─────────────────────────┘
Question 8: Sketch: \(y\,=\,\frac{1}{2}\left( 1 \,+\,f\left( 2x \right) \right) \)
Clue:
Re-write so the term with x is on the left:
y = +½ + ½f(2x)
└─┬─┘└───┬────┘
│ ┌───┘
└──┼─────┐
┌────┴─┐┌──┴─┐
y = ½f(2x) + ½
The Χ2 is INSIDE the brackets, so it stretches the curve by ½ along x
The Χ½ is OUTSIDE the brackets, so it stretches the curve by
along y
The +½ is OUTSIDE the brackets so it translates the curve up by
Question 9: Sketch: \(y\,=\,2f\left( \frac{1}{2}x\,+\,1 \right) \)
Clue:
Again, we encounter the "MULTIPLE TRANSFORMATIONS IN THE BRACKETS problem:
x ─────────► Χ½ ─────────► +1 ─────────► f(x) ────────► Χ2
╘═════════╤════════╛
│
┌───────────────┴────────────────┐
┌──┘ You can see that there are TWO └──┐
│ transformations INSIDE the brackets! │
└──────────────────┬───────────────────┘
│
Well - the SOLUTION IS SIMP│E, you just REVERSE the order of those TWO:
│
┌─────────┴───────┐
x ─────────► Χ½ ─────────► +1 ─────────► f(x) ─────────► Χ2
╘═╤═╛ ╘═╤═╛ ╘═╤╛
│ ① │
│ │
② │
│
③
Here's an applet for you to check: DON'T SAY I DON'T GIVE YOU NUFFIN'!
Question 10: Sketch: \(y\,=\,10\, -\,3f\left( 1 \,-\,x \right) \)
Clue:
Writing with the x term first:
y = -3 f(1 - x) + 10
Even inside the brackets - writing with the x term first:
y = -3 f(-x + 1) + 10
There are quite a lot of transformations do do here, AND, this one is TRICKY
We gotta be sure we do them IN THE CORRECT ORDER!
╔══════════════════════════╗
╔═════════╝ ⬡⬡⬡ When there are ⬡⬡⬡ ╚═════════╗
╔═════════════╣ MULTIPLE TRANSFORMATIONS INSIDE THE BRACKETS ║
║ ╚═════════╗ DO them in reverse order ╔═════════╝
╒═══╩═══╕ ╚══════════════════════════╝
y = -3f(-x +1) + 10
▲ ▲ ▲ ▲ ▲
│ │ │ │ │
│ │ │ │ │ ╒═════════╕┌──────────────────────────────┐
│ │ │ │ │ │ ┌─►──┤ +1 is inside the brackets: │②①
│ │ └───────►─────═╗ ┌─┘ ▲ │ shifts the curve left by 1 │
│ │ │ │ ┌─║─┘ ║ ╞══════════════════════════════╡
│ │ └──►────┘ ╚══╗ ▼ │Χ-1 is inside the brackets: │①②
│ │ │ │ └──►──┤ reflects curve in the y-axis │
│ │ │ ╘════╦════╛└──────────────────────────────┘
│ │ │ ╚═════ YOU CAN SEE I SWAPPED 'EM
│ │ │
│ │ │ ┌────────────────────────────┐
│ └─────────────│────┤ Χ3 is outside the brackets │③
│ │ │ stretch by
parallel to
│
│ │ └────────────────────────────┘
│ │ ┌───────────────────────────────┐
└────────────────│──────────┤ Χ-1 is outside the brackets │④
│ │ reflects curve in the x-axis │
│ └───────────────────────────────┘
│ ┌───────────────────────────────┐
└────────────────┤ +10 is outside the brackets │⑤
│ translates the curve
by
│
└───────────────────────────────┘
Complete this web lesson on separate paper from any other homework
The pass mark (to avoid additional homework on this topic) is: 8/10
Show full workings and highlight your answers
|
|






