Web Lesson 3: Force Diagrams
Force Diagrams
Really, the first thing you need to be able to do to get
anywhere with mechanics - is to be able to draw accurate force
diagrams...
There are numerous forces that can act on an object: Here are
the main ones we'll need to know:
1) Weight: Labelled $W$ or sometimes
$mg$
Any object on the Earth has a weight.
Like all forces, weight is measured in Newtons (mass is
measured in $kg$ and $mass \times gravity \;=\; mass \times
9.81$ gives the $weight$ of an object. We can approximate
$g$ as
$9.8$ and sometimes even as $10$ (if we want just a rough
answer)...
Weight always acts vertically downwards...
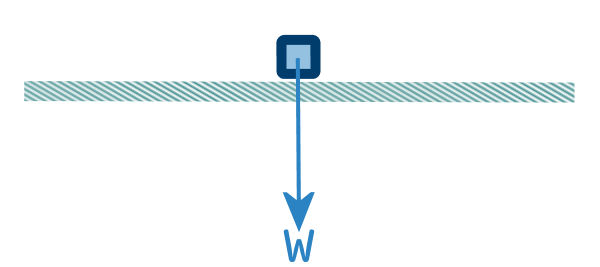
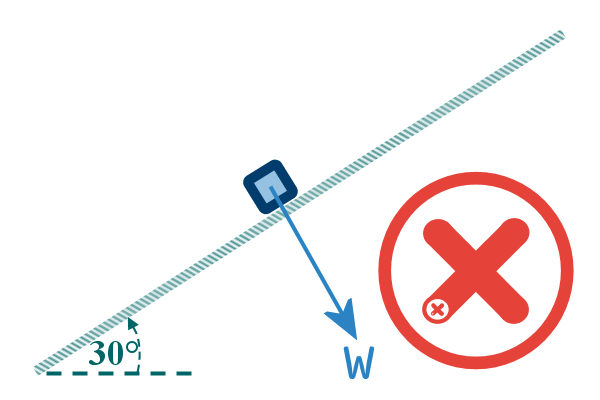
A common mistake, when the object is on a slope, is to angle
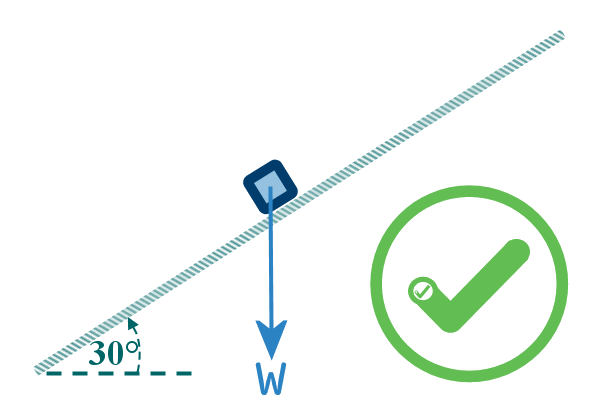
the weight incorrectly:
It must still act vertically downwards:
Not at some freaky angle:
2) Reaction: Labelled $R$
When an object is resting on a surface, then there is a
reaction force from the surface. If you stand on a surface
(such
as ‘the floor’ or a ‘table’, or your ‘dad’) then
your weight is pressing down on that surface. If you are
standing on your dad right now, he'll be able to give you a
colourful description of the effect of your weight pressing down
on him.
Now the surface you are on doesn't move despite the fact
that you are pressing on it (well, you dad might
move). That's
because the surface is strong enough to support you. It provides
a reaction force...
You are so used to these two forces (your weight, and the
reaction force of the surface) that mostly, you are oblivious to
them...
But if for some reason you are standing on a surface
that might-not support your weight, then you'll suddenly become
aware of the precarious reaction force - for instance if you are
crossing a creaky rope bridge with rotten wooden slats...
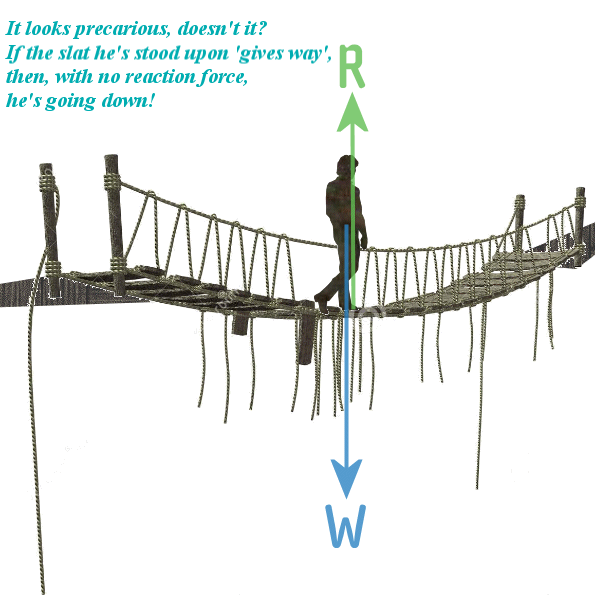
...you'll
creep ever so gently from one slat to the other, aware that if
one breaks (and so fails to keep providing the reaction force
your life depends upon) then you'll fall screaming into the
gorge below... Nice knowing you!
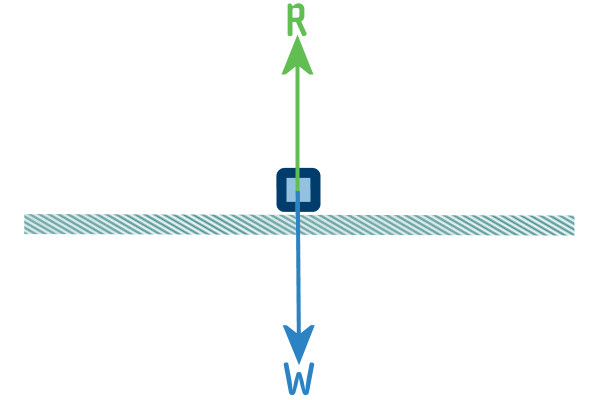
So, if an object is on a surface, then there's a reaction
force
Reaction force always acts at 90° to the surface
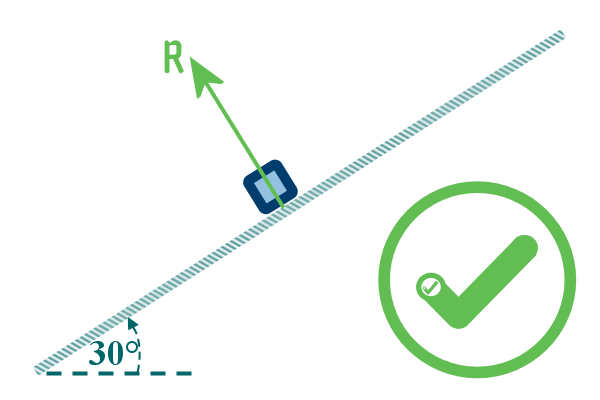
Which means when an object sits on a slope, then the reaction
is 90° to the slope, like this:
Sometimes, students mistakenly draw the reaction
force like this:
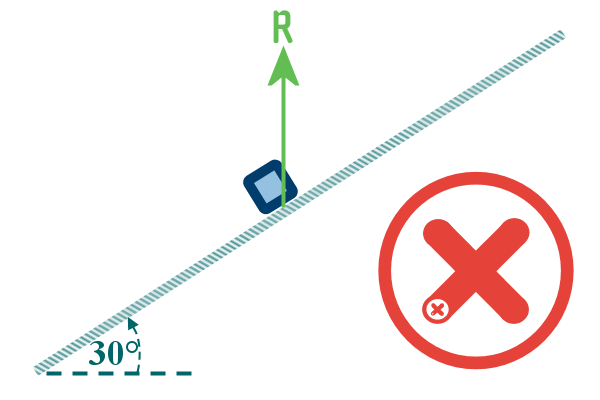
My reaction to students that make mistake is
not pleasant...
It is not just when an object is sitting on a surface that
the surface will provide a
reaction force - if you push hard against the wall then it will
push back by the same amount - that's still called a reaction
force.

So, when a ladder is put against a wall, then there are two
separate reaction forces to consider; one from the floor and one
from the wall...
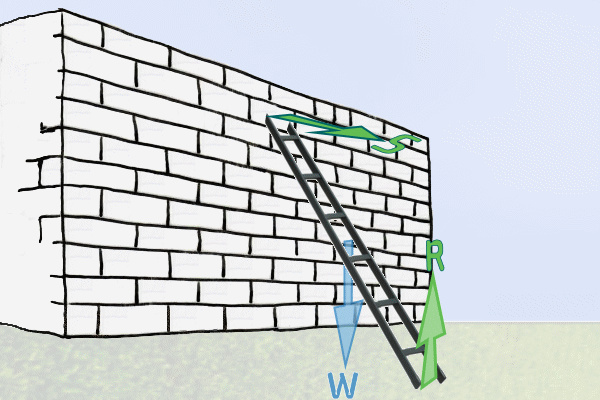
So, I labelled one of the reaction forces as $S$
(I can't label them both as $R$)
My attempt at the 3-D diagram isn't perfect, so just to be
clear - the force marked $S$ is perpendicular to the wall
3) Tension: Labelled $T$
If you want to pull a car, you might attach a tow rope to it
and pull the rope (especially if you are a competitor in the
World's Strongest Man). All the rope does is to transfer the
force you apply to the car:
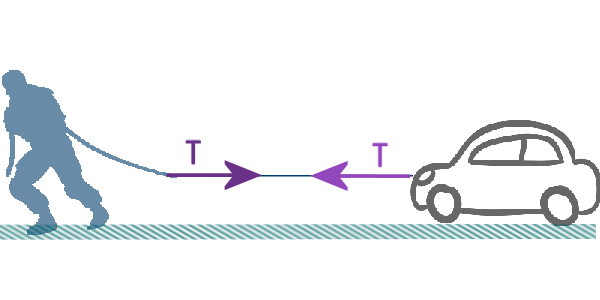
Why did I draw TWO tensions (in opposite
directions)?
Well, imagine you are the car, just sitting still minding
your own business, enjoying relaxing in the sun. Then some
geezer who want to prove he's ‘the World's Strongest Man’
attaches a rope to you and starts pulling you - you feel the
force of the rope pulling you to the LEFT (in my
diagram)...
Now imagine you are the competitor - you desperately want to
win ‘the World's Strongest Man’ competition, because it will
enable you to feel less of failure (you weren't good at maths,
and that has always been a disappointment to your parents, both
of whom were maths teachers...). All you need to do is to pull
this car 100m and you'll win. But try as hard as you can, it
won't budge. You are pulling to the left, but it feels like
there's a force pulling to RIGHT! (I think someone left the
brakes on)
So - the car experiences the tension pulling it to the LEFT
But the guy experiences the tension pulling to the RIGHT and
stopping him getting to the finish line...
Which is why I've drawn the tension going in both directions!
In a game of tug-of-war, both sides are pulling the rope in
opposite directions. Each team experiences a force from the
rope, but in opposite directions. The team on the left feel to
rope pulling them to the RIGHT and the team on the RIGHT...
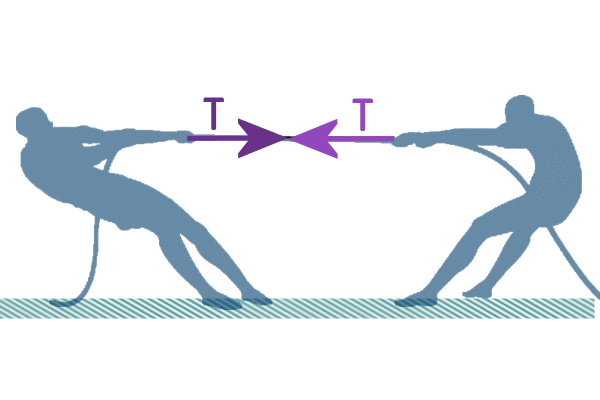
So, tension always acts along the rope/string, and in both
directions:
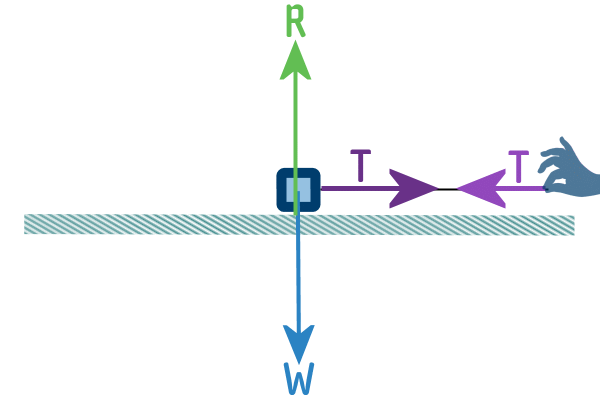
But we only need to draw it acting in the direction in which the
object (the one that we are concerned with) experiences it
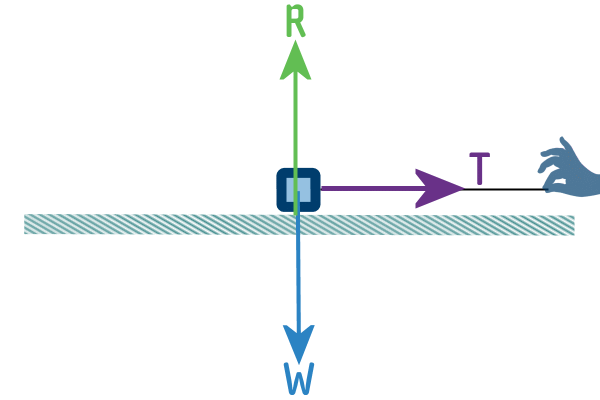
4) Friction: Labelled $F$
Friction is a force that opposes motion. Imagine dragging
your little brother across the floor. But he doesn't want to be
moved, so he tries to claw the carpet to make it harder to move
him. He's finding a way of increasing the amount of
friction
Now imagine you were pulling him across a smooth ice-rink
(you've got toothed-shoes, so you are able to grip on the ice).
It would be much easier to pull him, because the ice is slippery
- which means there's less friction... You laugh at him feebly
trying to claw at the ice...
There will always be some friction; but to make it simpler,
we sometimes decide to ignore friction completely. In that case,
we say the surfaces are smooth...
But, if we say the surfaces are rough, it means the
friction
must be included.
Friction only kicks in when the object tries to move, and it
acts in the opposite direction
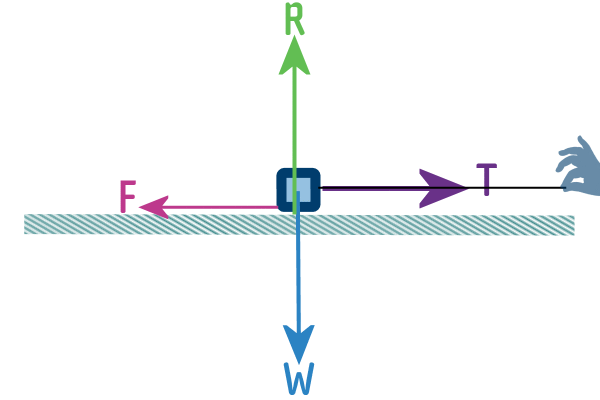
So when an object is pulled along a rough surface, to the
right in the case below, then the friction acts to the left...
If the object is sliding down a slope, then again, the
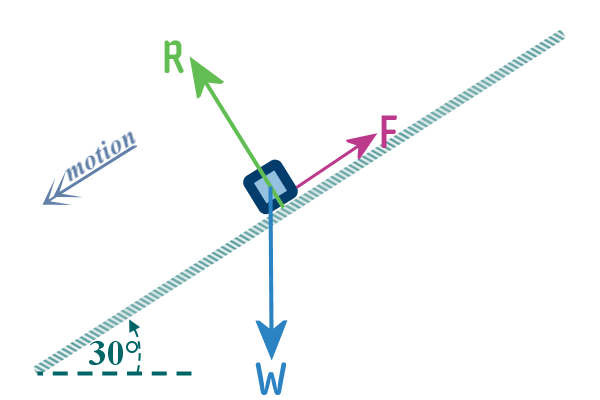
friction is saying ‘NO’, so it acts up the slope:
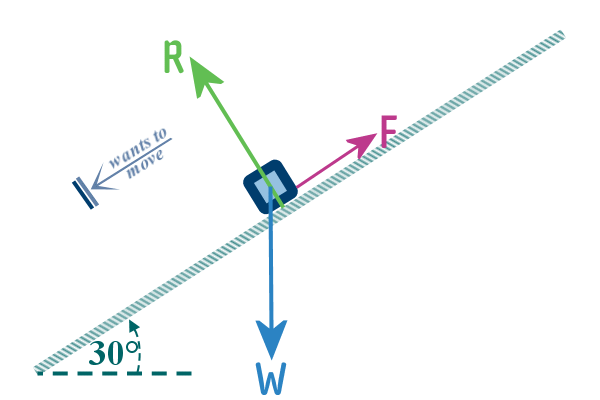
In fact, the force diagram would be the same in the case
where the friction was strong enough to hold the object on the
slope. The only difference would be that there would be no
motion - but we will usually say in that case, it is ‘on
the point of moving’ down the slope...
In that case, somewhere above the
object, mark the
direction which it is ‘on the point of moving’ using using a
combination of an arrow and a stop sign, like this: $\dashrightarrow \parallel$,
or like this $\parallel \dashleftarrow$:
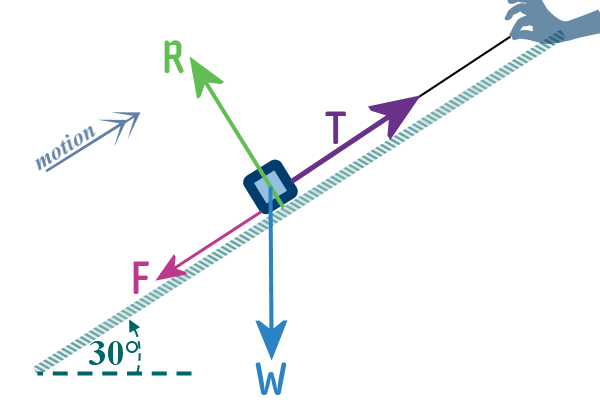
If we decide to pull the particle UP the slope, then friction
would say ‘NO’ to that as well. But this time, friction would act
down the slope in a pathetic attempt to stop us from moving the
object. But
we is stronger!
Free-body Diagrams
So, our Force Diagrams can become incredibly complicated if
ALL of the forces that are acting are drawn in:
For instance is we have an object being pulled up a rough
slope, and we draw every force, we end up with something like
this:
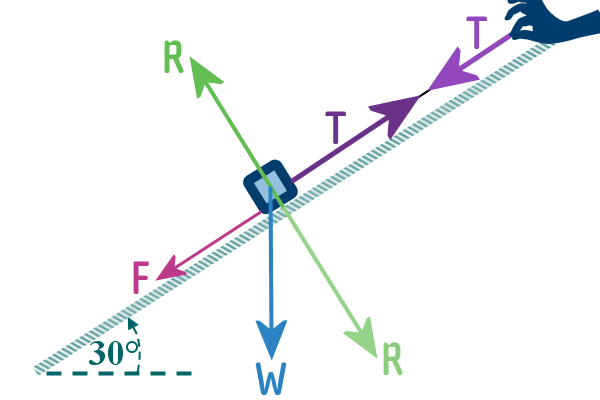
So, to avoid all that unnecessary complication, we revert to Free-body Diagrams
In a Free-body Diagram, we concentrate on just ONE object,
drawing it, with all the forces that act on it...
In the example above, it is the object on the slope that
we
want to focus on:
First, remove forces that the object exerts on other objects,
so we are just left with the forces that act in the object - so
below, I've removed one of the reaction forces and one of the
tension forces:
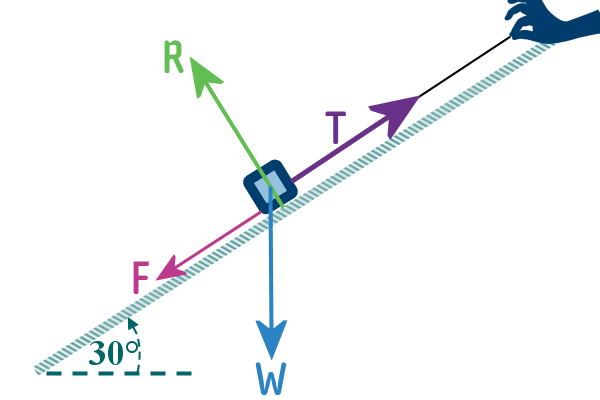
Finally, the external environment (the other objects, the slope on which the object
sits and the string attached to the object) are all omitted,
rubbed out, or just drawn in faintly in pencil...
So, our Free-body Diagram for the same situation, focussing
on the object on the slope, would look much simpler:
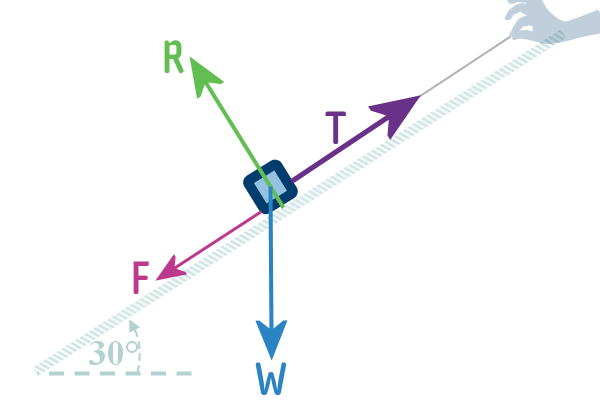
Free-body diagrams allow us to
analyse an object in isolation without distractions (I mean
distractions on the diagram; your snapchat feed is still going
to distract you!)
Once we are able to draw them correctly, we'll be able to
work out the sizes of the forces acting on the body, and/or the
velocity and/or the acceleration of the body
Let's use an example to work through the STEPS needed to
draw a correct Free-body diagram:
e.g. Sketch a Free-body Diagram to represent a car driving
up a hill at steady speed, experiencing some resistance to
motion
1. Sketch, $in\;pencil$, what is happening,
and decide which object you are concerned with
Read the situation carefully, to be certain you've
understood what is going on
Then sketch a representation of the object in its
environment
Representation means that, if the actual situation
describes a car driving at steady up a hill:

Then our representation would treat the car as a
single ‘blob’ (that's not the technical term; which would be
‘particle’)
And the slope is just treated as an ‘inclined plane’
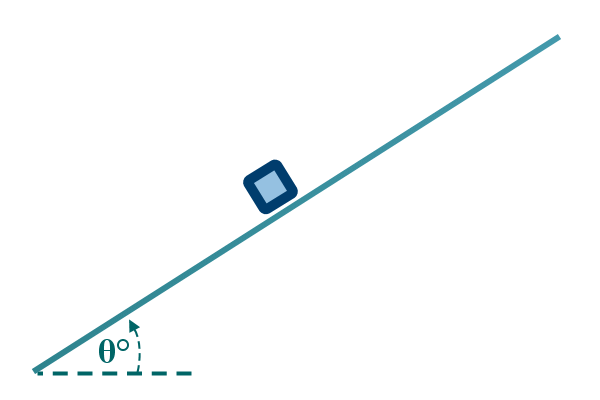
If the slope is ‘rough’, we might indiate that by using ‘hatching’
below the line of the slope:
2. Using SOLID-ARROWS ($\blacktriangleright$)
indicate all of the forces that act on the object
In pretty much every question, the first force we will need
to include is the weight. In order, the forces we would consider
are:
-
Weight $W$ or $mg$
-
Reaction: $R$ (if the object is on a surface)
-
Tension: $T$ (if the object is being pulled by a string/rope/rod)
-
Friction: $F$ (if the object is
moving, wants to move, or if some attempt to move the particle is being made)
-
Air resistance or ‘Drag’ $D$
(if the object is moving fast enough that air
resistance cannot be ignored)
-
Push/Pull $P$ (if the object is being pushed/pulled by an
external force, including the force supplied by the engine -
which seems paradoxical - how can the engine-force an ‘external
force’, but it will make sense when we've learnt
more)
Where it is possible to do so, try to represent BIGGER forces
with LONGER
arrows
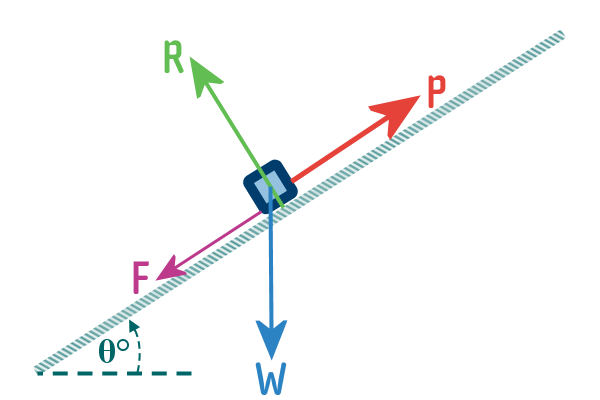
3. Use OPEN-ARROWS above the object to indicate MOTION
If you know that the object is:
Stationary ($\dashrightarrow \dashleftarrow$), and/or
Moving left ($\longleftarrow$), RIGHT ($\longrightarrow$), DOWN
the slope ($\swarrow$), UP the slope ($\nearrow$) etc, and/or
Accelerating ($\twoheadleftarrow$ or $\twoheadrightarrow$)
Then show that using the appropriate OPEN-ARROW
NOTE: Forces are drawn with SOLID ARROWs
($\blacktriangleright$),
motion is drawn with an OPEN-ARROW
($>$) and acceleration is
drawn with a DOUBLE-OPEN ARROW ($\gg$)
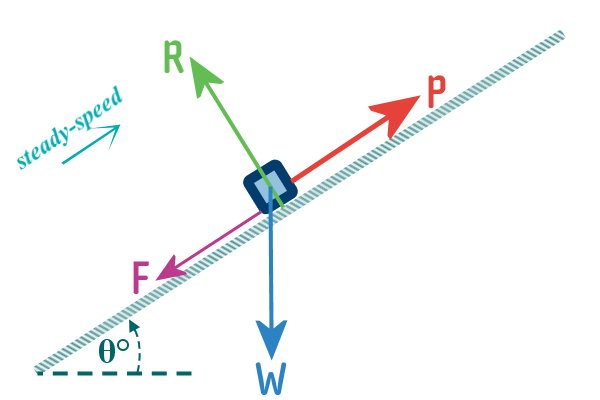
Sometimes, we have a situation where
the object is being force to more in a particular direction, but
the force is insufficient to shift it. In that case, mark the
direction which it is ‘on the point of moving’ using using a
combination of an arrow and a stop sign, like this: $\dashrightarrow \parallel$,
or like this $\parallel \dashleftarrow$
4. Draw the object in isolation
with the forces that act on it
Okay, so now it is time to highlight (in pen) the bits we need
to focus on - the object we are concerned with and the ofrces
acting on that object...
If your diagram has objects other than the one we are
focusing on, don't go over those in pen
Also don't go over the environment, such as the surface that
the particle is sitting on, in pen
What you'll end up with is this:
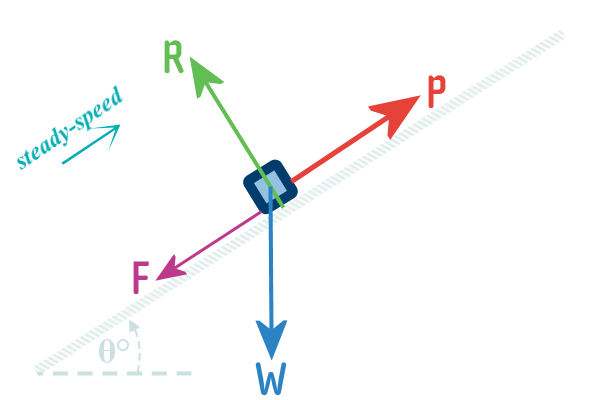
Examples:
Example 1: A 2000 kg SUV is being pushed at steady speed along a
horizontal road, by an angry man
The situation looks like this:
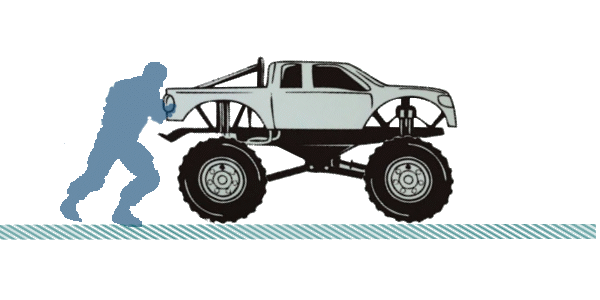
But our representation of the situation looks this:
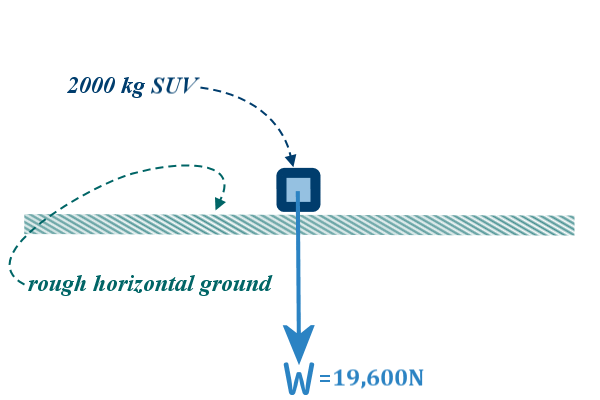
I've already drawn in the weight, which I've found by
multiplying the mass ($2000 \;kg$) by gravity ($9.8$) to get
$19,600\;N$, but it is okay to just write $2000g$ (everyone
will know that $g$ stands for $gravity$ which is $9.8$)
Now, we add in the rest of the forces:
NOTE: When a force is pushing/pulling
an object, we have a
choice of how to draw the force:
We could draw the PUSHING FORCE like
this (which is how we think of it when
we imagine the angry man behind the car pushing it):
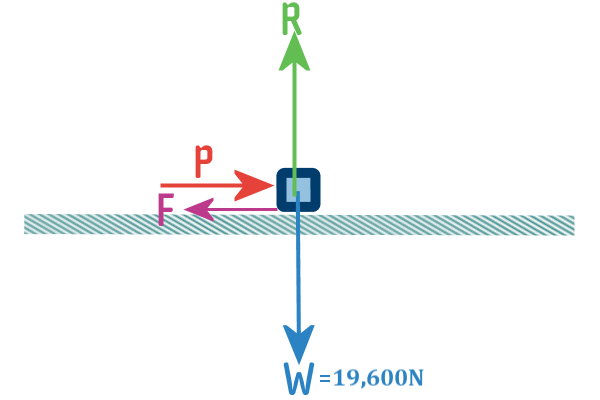
Or we can draw it like this - which is effectively exactly
the same force (it is the same size and
it is pointing in the same direction!):
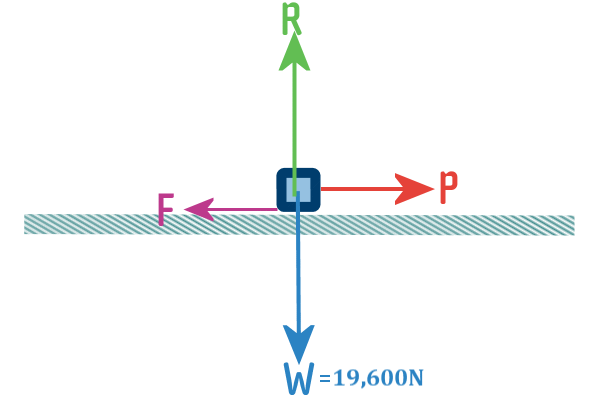
We prefer the second version, where all of the forces are drawn
coming out of the object
Next, since we know the object is moving (but not
accelerating), we draw an arrow to show the motion:
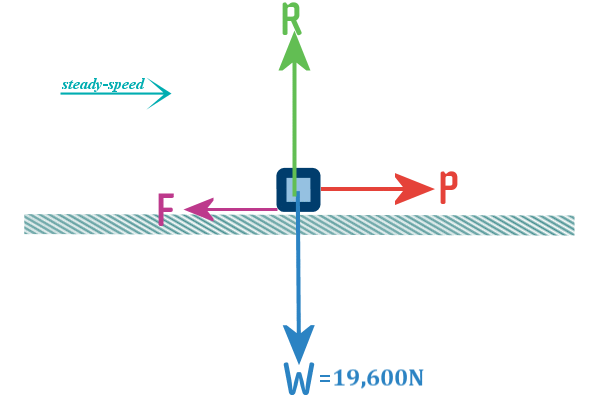
Finally, since we are after a Free-body
Diagram (of the car),
we can rub out the surface on which the car is travelling:
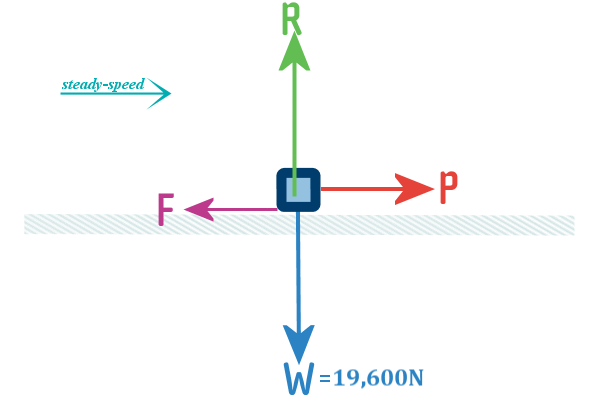
Job done!
Example 2: A 20 kg bike is hanging from two ropes attached to the ceiling. The first rope makes an angle of
40° with the ceiling, while the second rope makes an angle of
60° with the ceiling
This is the image I have in my bike - yes, with lovely a PINK
bike
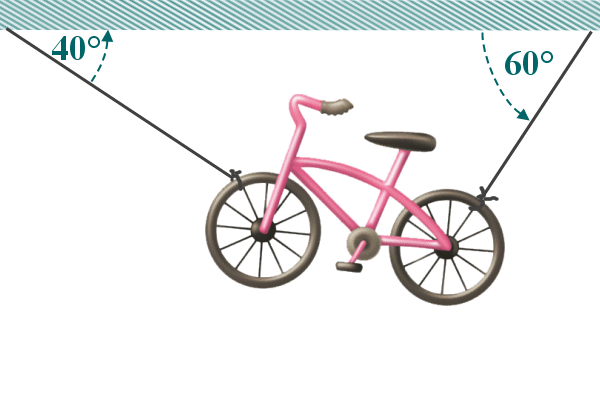
But our diagram simplifies the bike by treating it as a
single ‘blob’ and the ropes are treated as light
inextensible strings (basically, that means they are straight,
whereas in reality, they might be slightly curved):
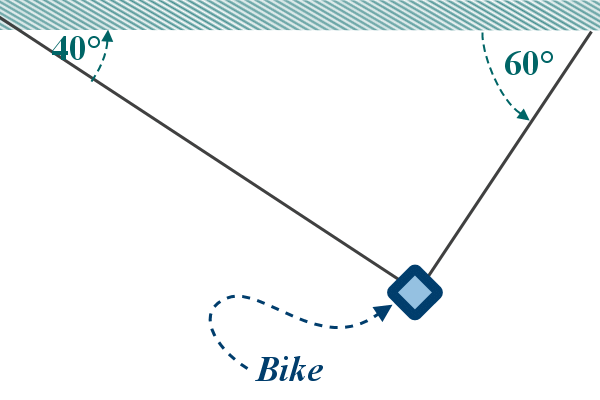
Now we know from the notes at the top, that every rope carries
TENSIONS in two directions
The bike feels both of the TENSIONS as acting sort-of-upwards...
...but the poor ceiling is feeling the force from the ropes
acting sort-of-downwards:
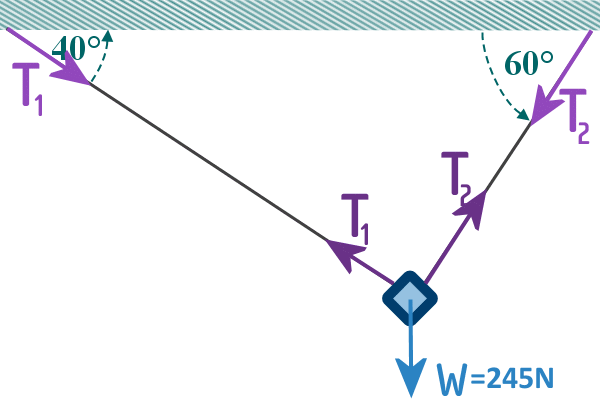
We are focusing on the forces on the bike, so we get rid of the
two tensions that the ceiling experiences:
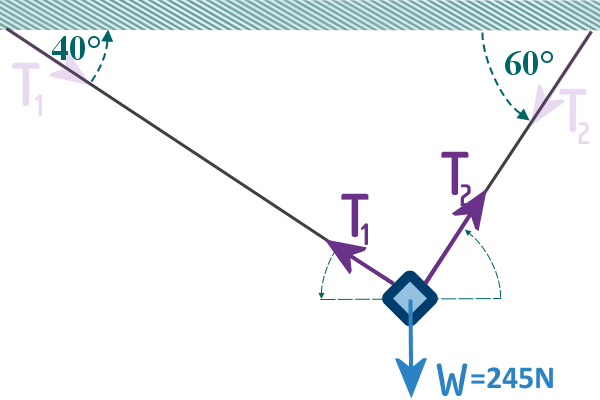
There's no need to have any ‘motion’ arrows or ‘acceleration’
arrows - the bike is in ‘equilibrium’
So the last thing to do is to get rid of everything except
the bike and the forces on it:
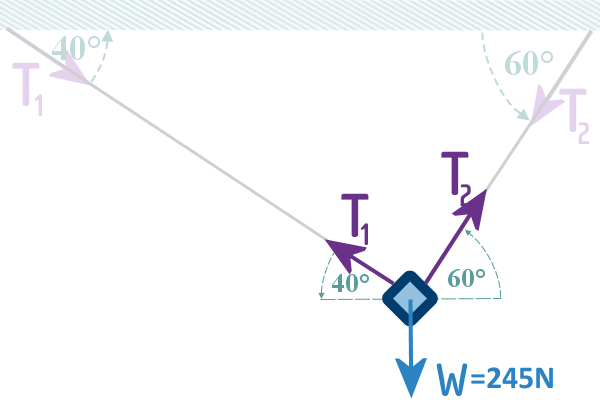
Note: It is perfectly okay to transfer those angles to where the
forces are coming out of the bike, since they are the angles
that the forces act along, which is a part of each force...
Example 3: A 50 kg parachutist is falling through the air
(with her parachute open) at steady speed.
How exciting - a parachute jump. Look how happy she is:

We are interested in the girl and the
forces acting on her. Obviously the first force we think of is
her weight (not in that way, we aren't judging). The other force
she feels is the force from the strings of the parachute holding
her (without them, she wouldn't be smiling). There's air
resistance too, but mainly, that acts on the parachute, not on
her...
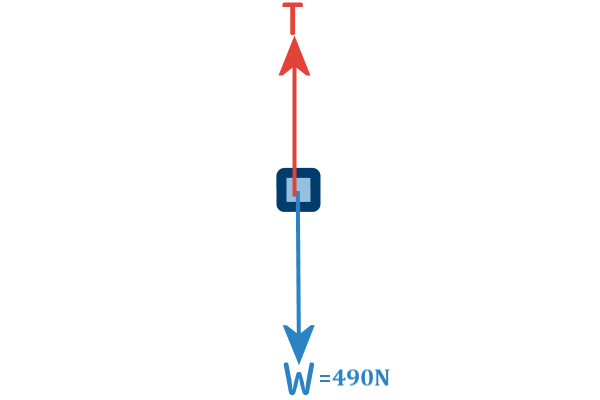
Notice I've drawn these forces as pretty much equal in length
- that's because if the TENSION was was much less than her
weight, then she'd be accelerating downwards and we don't want
that!
The last thing to do is to add in an OPEN-ARROW to show she
is moving at steady-speed
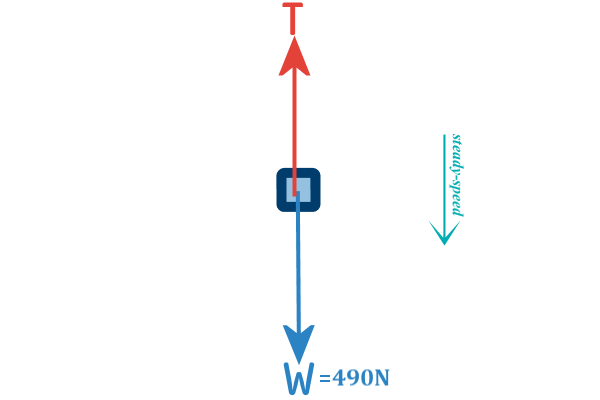
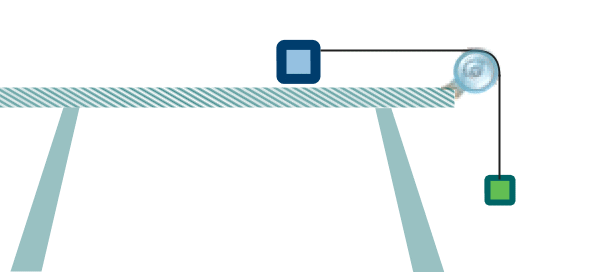
Example 4: A 2 kg particle is on a rough horizontal table.
It is connected by a string, which passes over a pulley (fixed
to the edge of the table) to another particle of mass 1 kg. When
released, the 1 kg mass drops and the 2 kg mass slides across
the table. Draw a FBD of the 2 kg particle
So, this is what it actually looks like:

But our representation simplifies it slightly:
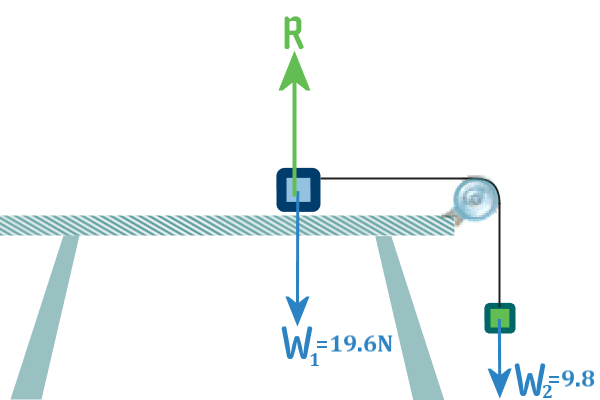
The first forces we can draw in are the weights (of each) and
the reacion (of the 2 kg particle - since it is on a surface):
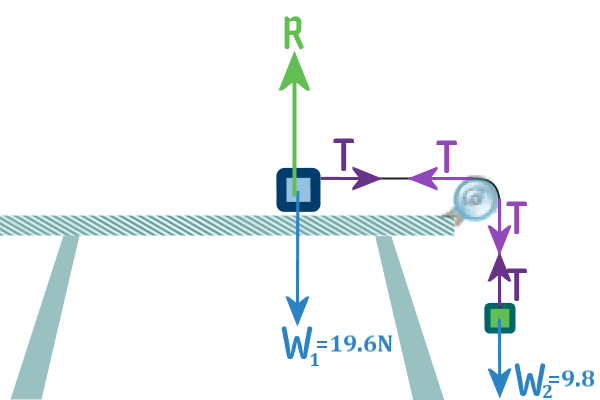
Next - the TENSIONS. We can think of the string as two separate
‘parts’ of string. And, in each part, we draw the tensions
acting in both directions (we know this from the rules at the
top of the page).
Here's the clever bit - if the pulley is smooth, then the two
tensions on one bit will be the same as the two tensions on the
otehr bit:
As usual, one of the tensions in each pair is no no interest to
us, so we can rub those out...
These objects are going to be moving to the RIGHT, but since
the table is rough, there'll be some friction opposing the
motion:
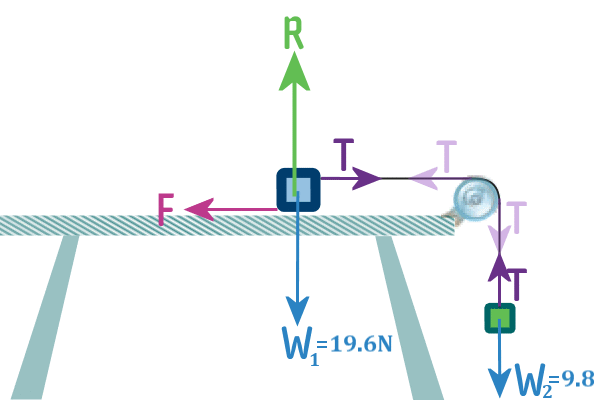
Now, the question says, when they are released, the 1 kg mass
starts falling. From that, we can conclude they are accelerating
- so I've added in TWO acceleration arrows - one for each:
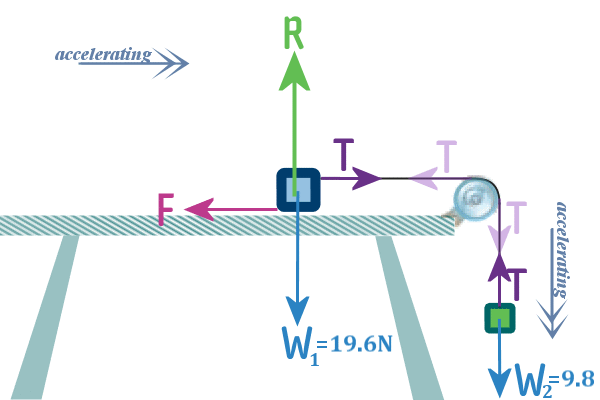
And lastly, since we are interested in the forces acting on the
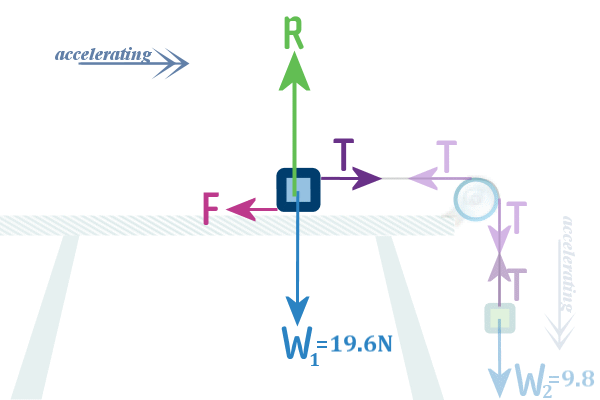
2 kg particle, I've rubbed everything else out:
Now complete the 10 questions below:
You can use g
= 9.8 m/s² or, for (for
ease of calculation) you may
use g = 10 m/s²
in these questions
Questions 1: A crate of mass 100 kg is being pushed
over a rough horizontal floor
Draw a FBD of the crate
Clues: Our representation would start off looking like this
(before any forces are added in):

The first force we would add in is the weight:
To calculate the weight we use: $weight \;=\; mass \times gravity$
We can approximate
$g$ as
$9.8$
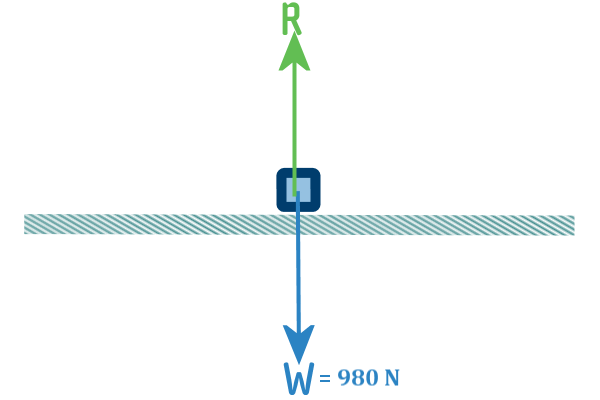
So we have: $weight \;=\; 100 \times 9.8 \;=\; 980;N$
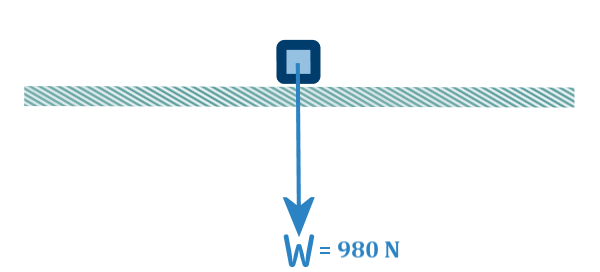
Since our crate The next force to add in is the $reaction$:
The reaction is always at 90° to the surface
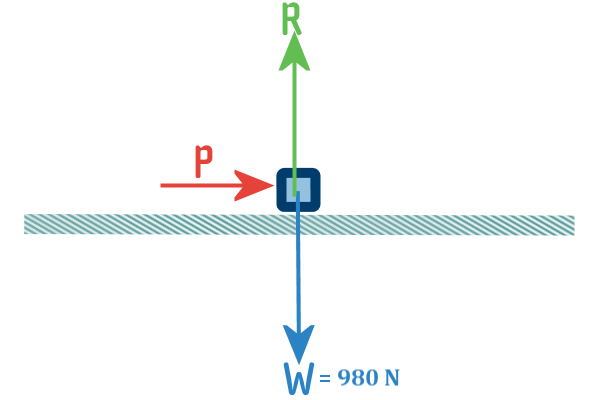
The crate is being pushed over the floor, so there must be
someone pushing it - let's add in a force, pushing it to the
right (actually, itdoesn't matter whetehr you draw it being
pushed to the right or to the left, but conventionally, we
prefer drawing thisngs being pushed to the right):
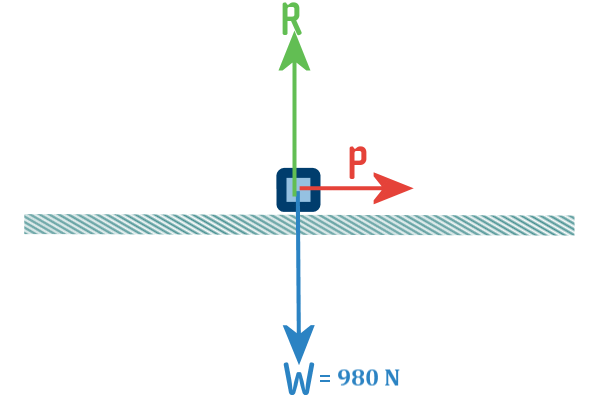
Although there is nothin wrong with this diagram, we do
prefer it if all of the froces acting on the particle are
pointing out of the particle...
...so let's keep that force pushing the the right, but let's
move it to here:
Next, it says the floor is ROUGH. That means we need to
include friction. Since we are pushing it to the RIGHT, friction
must act to the LEFT (because friction always acts in the
opposite direction to motion - in Gujarati, we call that ‘aadouh’)
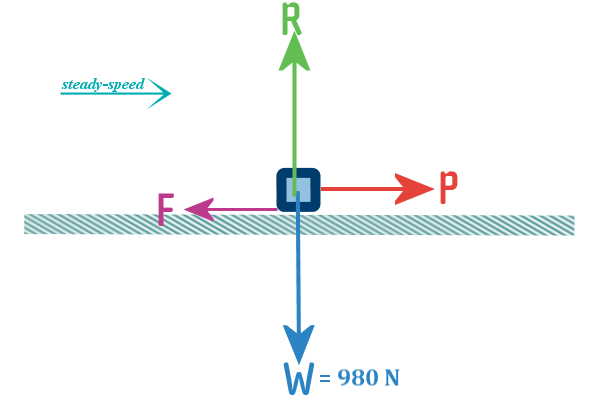
And while I was adding in that last force, I also added a
open arrow showing that the crate was moving to the right
I assumed steady speed (even though it didn't speficially say
that in the question) - that is a reasonable assumption!
Finally, our F.B.D doesn't really need to include the floor,
so I'll rub that out now...
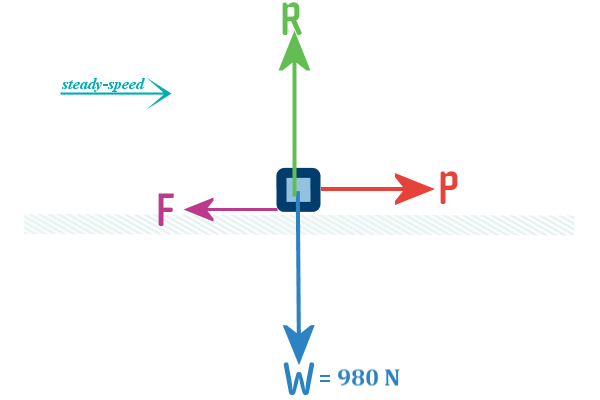
There - that's our answer...
Question 2: A 1 g feather is falling through the air, pretty
much at steady speed
Draw a FBD of the feather
Clues: This time there's no surface to include at all...
But there's nearly always a weight to include - even for
something that is ‘as light as a feather’
The feather's weight can be found by: $weight \;=\; mass \times gravity$
We can approximate
$g$ as
$9.8$
So we have: $weight \;=\; 0.001 \times 9.8 \;=\; 0.0098;N$,
or you can just write: $weight \;=\; 0.001g$
There is one other force we need to consider - which is
air-resistance. For a featehr falling through the air,
air-resistance is a big deal (which is why, if you drop a
feather from the top of a tall building, it just glides gently
down to the ground; whereas, if you drop your friend from the
top of a tall building, they'll accelerate and accelerate until
they splat onto the floor at a tremendous speed...)
Finally, we can draw in an arrow showning the feather moving
downwards at steady speed...
Question 3: A 500g ball is thrown vertically upwards
Draw a
FBD showing the ball on its upward path. Ignore any air
resistance
Will the diagram change for the downward path?
Clues: This is like the previous question, except for the the
fact that this time, we are told to IGNORE air resistance!
So, there is ONLY ONE FORCE acting on the ball...
The ball is moving UPWARDS, but the only force on the ball is
acting downwards, so that means it must be accelerating
downwards...
What does that mean - "the ball is moving upwards,
but accelerating downwards"?
To answer that, you need to know that:
┌──────────────┐ ┌────────┐ ┌──────────────┐ ┌────────┐
│ ACCELERATION ├─►─┤ to the │ ≡ │ DECELERATION ├─►─┤ to the │
│ OF 2 m/s² │ │ RIGHT │ ▲ │ OF 2 m/s² │ │ LEFT │
└──────────────┘ └────────┘ │ └──────────────┘ └────────┘
│
equivalent
Similarly:
┌──────────────┐ ┌────────┐ ┌──────────────┐ ┌───────┐
│ ACCELERATION ├─►─┤ DOWN │ ≡ │ DECELERATION ├─►─┤ UP │
│ OF 10 m/s² │ │ WARDS │ ▲ │ OF 10 m/s² │ │ WARDS │
└──────────────┘ └────────┘ │ └──────────────┘ └───────┘
│
equivalent
So, instead of saying,
"the ball is moving upwards
with a speed of (say) 25 m/s and an acceleration downwards
of 10 m/s²"
We could say,
"the ball is moving upwards
with a speed of (say) 25 m/s and an deceleration of 10 m/s²"
This makes more sense now - the ball is moving upwards, but
it is slowing down... That's what happens when you throw a ball
upwards (until of course, it starts a downwards path)
So, our diagram needs to include a speed arrow (pointing
upwards) and an acceleration arrow (pointing ___wards)
Question 4: A 100g sponge-ball is thrown vertically upwards.
This time don't ignore air resistance
Draw a FBD showing the
ball on its upward path. Will the diagram change for the
downward path?
Clues: We have no surface...
We have a weight of $0.1g$ or $0.98\;N$
We have some air-resistance: This acts downwards
(air-resistance is like friction, it acts in the opposite
direction to the direction of motion)
The ball is moving upwards, but it will be decelerating...
So we need to include a speed arrow (pointing ___wards) , and
an acceleration arrow (pointing ___wards)
Question 5: Joseph is gently guiding a wheelbarrow down a 40°
slope. He has to ensure the wheelbarrow keeps moving at a steady
speed, and doesn't ‘run-away’
Assuming there is friction, draw a free-body diagram of the
wheelbarrow
Clues: That's quite a steep slope that he's trying to guide
the wheelbarrow down - I don't rate his chances...
So this is sort of what the situation looks like:

We wanna draw a FBD of the wheelbarrow - so let's represent
the wheelbarrow as a blob:
And of course, let's include its weight (which we don't
know):
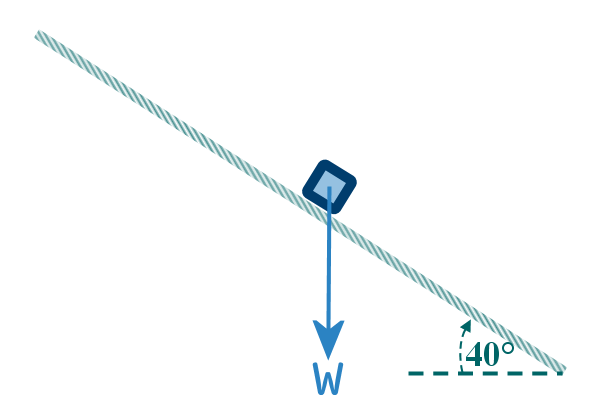
And, since it is on a surface, lets show the reaction force:
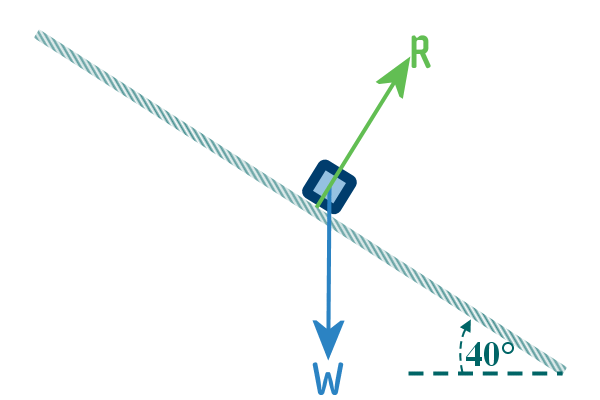
Now, Joseph must be exterting a force in the direction UP THE
SLOPE, because otherwise, the wheelbarrow would simply run-away
down the slope at a very quick rate...
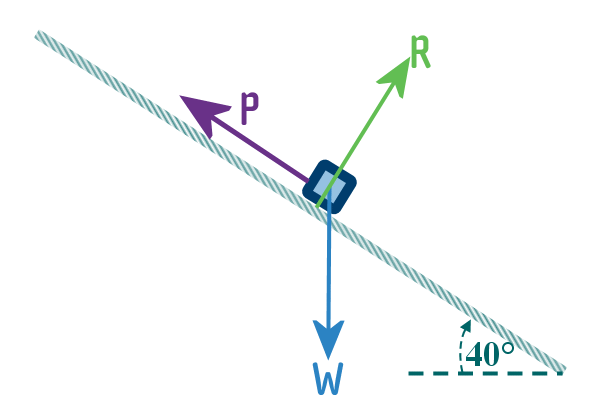
It tells us to include friction...
...which always acts in the opposite direction to the motion.
And we need to show an open arrow for the steady speed.
Question 6: Mike has fired a bullet at a softwood target. He
knows from past experience that the bullet will penetrate around
20 cm intothe wood
Draw a FBD of the bullet as it is passing
through the wood
Clues: The actual situation looks a bit like this:

And our representation will look like this:

The bullet has a weight, and I'm going to show that on the
diagram, but we need to remember that, compared to the otehr
forces, the weight of the bullet is going to be tiny...
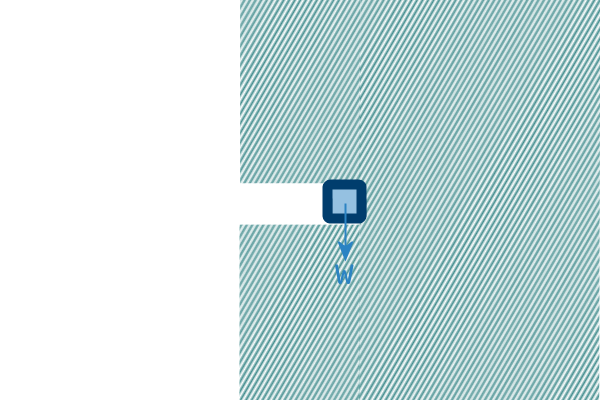
And there'll be a small vertical reaction force (which is
about the same size as the weight - and really not an important
force)
The BIG force in this situation, is the force from the wood -
acting to the LEFT) slowing the bullet down. You can call that
force a RESISTANCE FORCE (sort of like a huge version of
friction), or you can call it a REACTION FORCE, it doesn't
really matter - but is is a big force and it is the force that
slows the bullet down and brings it to a stop...
Note: Students often think there must be a force acting to
the RIGHT, because the bullet is heading to the right. But
remember, we are interested in the forces acting ON THE
BULLET.
Question 7:
Fred is moving home and he wants to take his grand piano with
him. However, it is upstairs and it is too wide to take down the
stairs. (No, I don't know how it got there either.)
Firstly, The
removals company remove his bedroom window, then they attach a
pulley to the top of the window frame
A rope is connected to
the piano, passed over the pulley and two removals men hold the
rope tightly.
The piano is then lowered out of the window and
the removals men are gently letting the rope through
their fingers to lower the piano steadily to the ground
Clues: The actual situation looks like this:
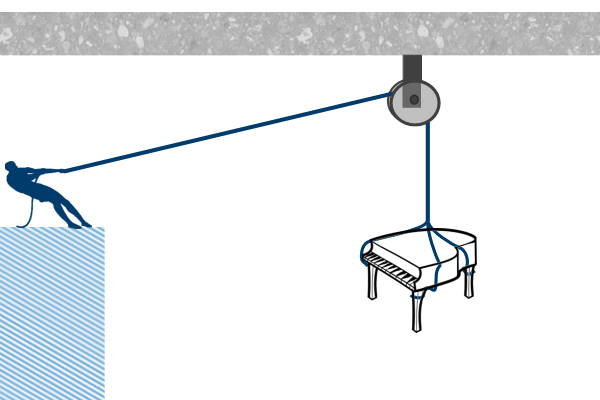
But we can represent the piano as a ‘blob’ (I mean a ‘particle’)
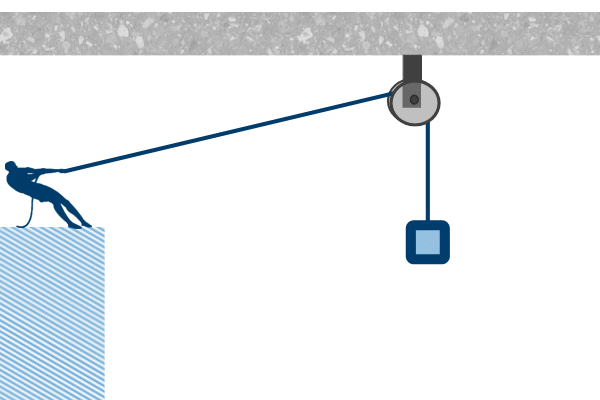
We can add inthe weight of the piano:
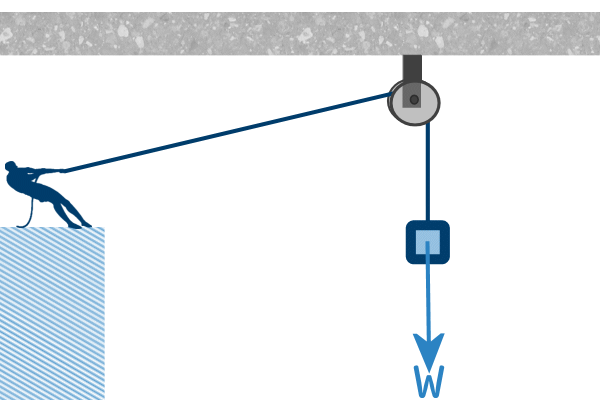
And the tension (which we know act in both directions):
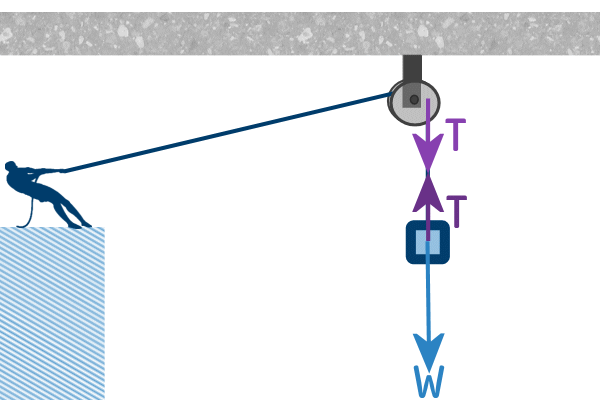
But, since we are only interested in the forces acting on the
piano, we only need the upwards tension.
And we can now run out everything else...
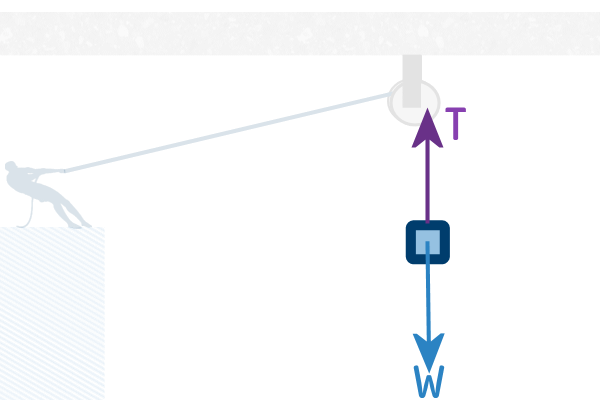
Don't forget to include an open arrow showing the piano being
lowered at a steady speed...
Quesiton 8: A 1000 kg car has broken down. A passing SUV
driver offers to tow the car to a nearby garage. A long tow rope
is connected between the cars and the SUV and then SUV pulls
away slowly.
They acclerate to 20 km/h (don't drive fast when
towing) along rough horizontal gorund.
Draw a FBD of the car
being towed.
Clues: So, the situation looks like this:
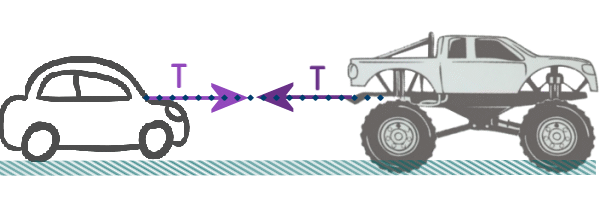
I've shown the tension in the tow-rope acting in both
directions (we know a tension acts in both directions)
Our ‘representation’ will treat each car as a ‘particle’:
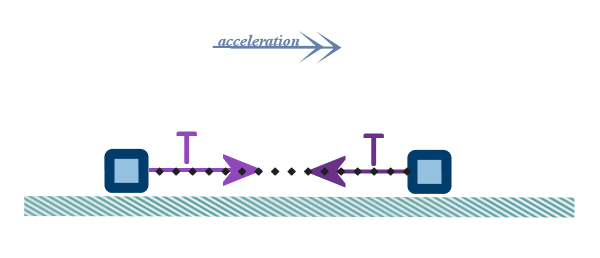
And each ‘particle’ has a ‘weight’ and a ‘reaction’
force from the surface. I've drawn the ‘weight’ and ‘reaction’
forces for the SUV as being much bigger than for the dinky
little car. Because SUVs are basically obese cars:

Now the SUV must be providing some thrust to pull itself and
the other car along. Quite a lot I guess, because they are
accelerating:
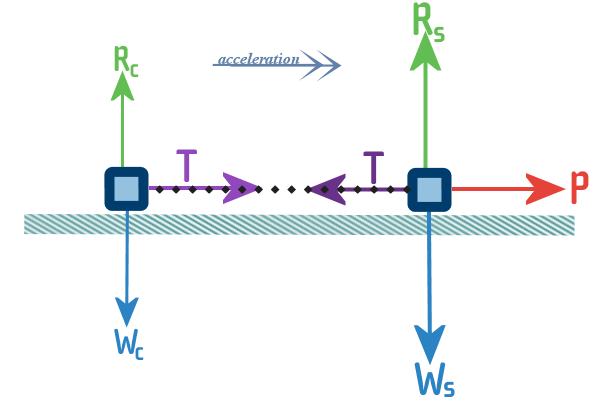
And both cars will have friction forces acting on the
opposite direction tothe motion:
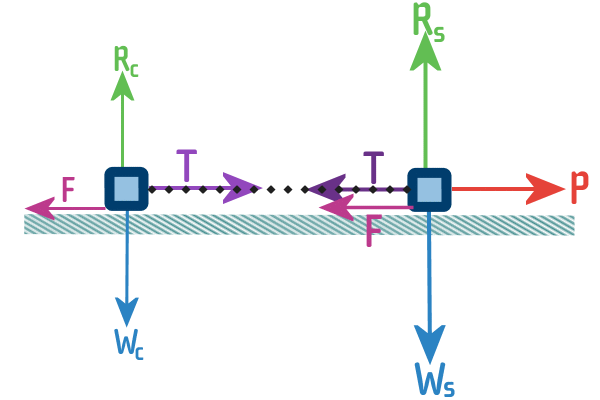
Finally, we wanna focus on the dinky car and not the SUV:
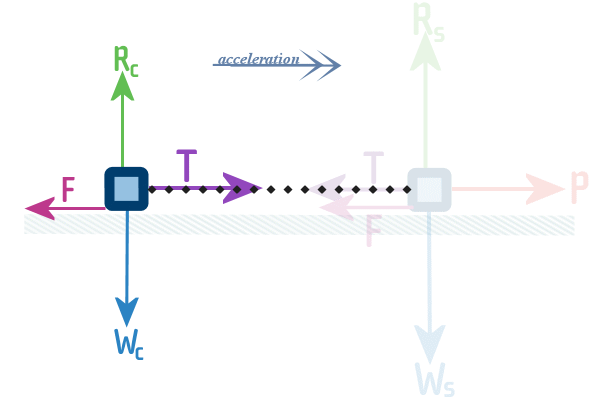
Question 9: A rectangular picture is hanging from a hook on
the wall. A long string is attached (one end to the top left
corner and the other end to the top right corner) to the picture
and then it is lung over the hook. The picture is hanging level,
as it should be.
Draw a FBD of the picture. Draw the picture. Draw a picture of you drawing the
picture.
Clues: The picture is hung from a string, attached to the top
corners - like this

Question 10: The back of a 10 cm wide shelf is fixed to to
the wall by a fixing bracket. But if heavy items are placed on
the shelf it will tend to sag at the front (try it - place some
really heavy objects, like your brother on a shelf that is only
fixed at the back - actually, no - DON'T try it, trust me!). So,
the shelf also has a string at either end, fixed from the front
of the shelf to a point on the wall 16 cm above the shelf.
Draw
a FBD of the shelf (while your brother is sitting on it).
Clues: Here's sort of, what the situation looks like:
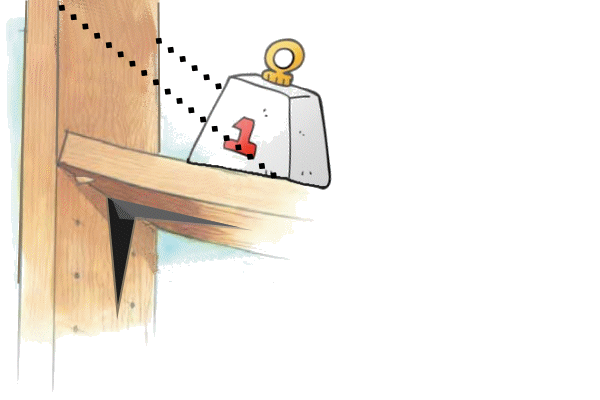
Our representation would look like this:
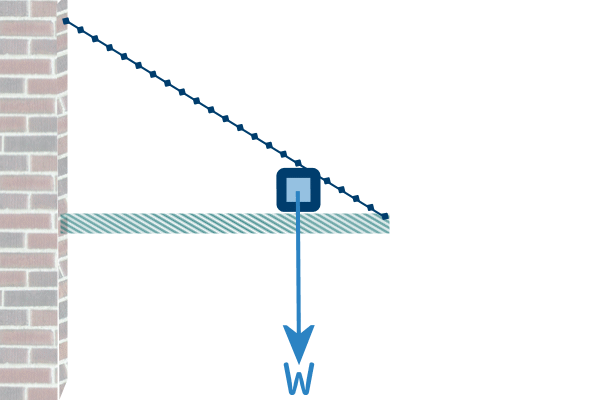
Question 11 (An extra ‘challenge’
question): Dina is standing in the lift on the ground
floor of the CN tower (it's a very tall building). She presses
the button to go to the top floor and the lift starts to
accelerate upwards - it's an amazing experience, a bit like
being on a rocket taking off from the launch-pad.
Draw two separate FBDs (one of Dina and one of the lift) during
the acceleration phase of her ‘take-off’
Clues: Sorry - no hints for this one...
|










































































