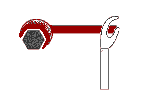
Exercise 8B

Moments and Equilibrium

'Turning forces' are called 'Moments'. Moments are measured in a new unit called "Newton-metres" (Nm):

Moments

Moment
(Nm)
 
=
Force
(N) 
 
×
 
Distance from pivot
(m)

 
In each case, we must identify the pivot (the point about which the rod will turn) and the force (a line along which the push or pull is taking place):

In every-day use, levers provide a greater moment. For example, imagine using a short spanner to unscrew a nut:

Now imagine using a longer spanner for the same job:

You know instinctively, that the longer spanner will make it easier. Now, knowing about moments can make that simple to understand. Imagine the maximum force your hand can exert is 200N and the spanner is only 10 cm long:

F = 200 N	╗
d = 0.1 m	╠══	Moment =   F × d
Moment = ???	╝	       = 200 × 0.1
		               =   20 Nm

But, using the longer (50 cm) spanner, our same 200N force produces a larger moment:

F = 200 N
d = 0.5 m

	Moment = 200 × 0.5 = 100 Mn
 
e.g: A car door has width 1.2 m and is hinged at one end
On the outside, there is a handle at the opposite end to the hinge. On the inside, there is a handle in the middle of the door
The door is stuck and so two people are trying to prise it open. Carlos is pulling the handle from outside using a force of 80 N. Jose is pushing the handle from inside using a force of 100 N
Find the total moment produced by the gruesome twosome
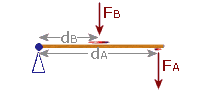	  There are two moments in this diagram:
 
 Moment due to Jose:
  
 FB = 100 N (Carlos)
 dB = 0.6 m
 
 MomentB =   F × d
         = 100 × 0.6
         =   60 Nm
 
 Moment due to Carlos:
 
 FA = 60 N (Jose)
 dA = 1.2 m
 
 MomentA =  F × d
         = 60 × 1.2
         =   96 Nm
 
 
	  Total Moment = 60 + 96 = 156 Nm
 

Equilibrium

In 'Forces and Motion we had to consider the forces acting on a particle. We needed to define which direction was positive and which was negative.

If the positive forces equal the negative forces, then we would say the particle was in equilibrium.

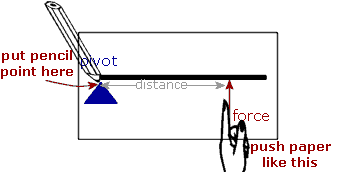
Since moments are "Turning Forces", we can't define "positive" and "negative", so instead we define which moments are "clockwise" and which are "anticlockwise":

To decide if a moment is clockwise or anticlockwise, put your pencil point on the pivot and pull the paper in the direction of the force.

If the paper turns "clockwise", then the moment is a "Clockwise Moment":

So, in this case the moment is "Anti-clockwise".

For moments, equilibrium occurs if the clockwise moments equal the anticlockwise moments

Moments: Equilibrium

Anti-clockwise Moments
 
=
 
Clockwise Moments

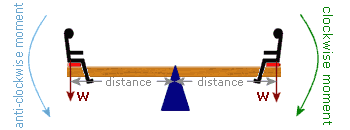
Take the example of a see-saw:

If a boy ("Henry") sits, on the right-side of the see-saw, then his weight will produce a "Clockwise Moment" (because his weight makes the plank turn in a clockwise direction):

Since there is no "Anti-clockwise Moment" to balance this, the see-saw will turn until it hits the ground:

If, instead "Henry" and his identical twin "Amritlal" both get on the see-saw:

Then there are two moments. Henry's weight still produces a "Clockwise Moment", but Amritlal's weight produces an "Anti-clockwise Moment" (because he is on the left-side of the pivot):

And, since they are both the same weight and are sitting the same distance from the pivot, the anti-clockwise moment equals the clockwise moment and the see-saw will remain balanced.

In practice, one of the twins will "kick-off" from the ground (providing an extra force which unbalances the moments) and that person will start to rise. Then the other twin will "kick-off" from the ground....

 

Weight of the Plank

Until now, we've ignored the weight of the plank in working out the moments. But, if the pivot is not placed in the centre of the plank, then we must also include the weight of the plank. This force is drawn onto our diagram as a vertical line placed halfway along the plank:

Now, as the questions become a little more detailed, it is VITAL to start with a clear diagram:

  • Decide where your pivot is and mark it with a "Δ"
  • Put in vertical arrows to show each weight (including the weight of the plank which acts from its centre)
  • Only label the distance of each weight from the PIVOT

Question 1: We need to add in the REACTIONS at each support:

 

Now, since the plank is in EQUILIBRIUM, we can take MOMENTS about any point, and say, "ACWM Moments = CWM Moments":

The TRICK is to always take moments about a point which has UNKNOWN FORCES

                     ◄─ Force through the PIVOT                        ◄─ A.C.W.M.
                        has ZERO moment - ignore!                      
                    
                       
    Take Moments 
    about ‘A’ ──►
                                             
                                                                 
                 
                                                   C.W.M ─►
                   C.W.M ─►
 
└─────────┬─────────┘         AT EQUILIBRIUM:        └─────────┬─────────┘
│                                                    │
└── ANTICLOCKWISE MOMENTS  =     CLOCKWISE MOMENTS ──┘
               (RB)×(…)  =   (15)×(…) + (10)×(…)

You see - by taking moments about ‘A’, we were able to eliminate the reaction force (${R}_{A}$) - which meant we could find ${R}_{B}$

Now, rather than take moments again - we can just use: $Forces\; \uparrow \quad =\quad Forces\; \downarrow$...

 

 

Question 2: We need to add in the REACTIONS at each support:

 

Now, since the plank is in EQUILIBRIUM, we can take MOMENTS about any point, and say, "ACWM Moments = CWM Moments":

The TRICK is to always take moments about a point which has UNKNOWN FORCES:

Force through the PIVOT ─►                                     ◄─ A.C.W.M.
has ZERO moment - ignore!           
                    
                       
    Take Moments 
    about ‘A’ ──►
                                             
                                                        
      A.C.W.M ─►
                                                                        ◄─ C.W.M.
                                               ◄─ C.W.M.
 
    
└─────────┬─────────┘         AT EQUILIBRIUM:        └─────────┬─────────┘
│                                                    │
└── ANTICLOCKWISE MOMENTS  =     CLOCKWISE MOMENTS ──┘
                (5)×(a) + (RB)×(a)  =   (20)×(2a) + (10)×(5a) ‹– cancel 
                                                                through

You see - by taking moments about ‘A’, we were able to eliminate the reaction force (${R}_{A}$) - which meant we could find ${R}_{B}$

Now, rather than take moments again - we can just use: $Forces\; \uparrow \quad =\quad Forces\; \downarrow$...

 

 

Question 6: We can take moments about ANY point (‘A’, ‘B’ or ‘C’) - but it helps to take moments about a point where an UNKNOWN force passes through - so I decided to take moments about ‘C’:

 Force through the PIVOT ─►                                              ◄─ A.C.W.M.
 has ZERO moment - ignore!                      
   
    
      
                              ▲
 Take Moments about ‘C’ ──────┘
                                                                      
                                 C.W.M ─►
 
└─────────┬─────────┘           AT EQUILIBRIUM:            └─────────┬─────────┘
│                                                          │
└──── CLOCKWISE MOMENTS    =   ANTICLOCKWISE MOMENTS ──────┘
(…)×(a)  =  (…)×(…)

Now, rather than take moments again - we can just use: $Forces\; \uparrow \quad =\quad Forces\; \downarrow$...

Note: In this question - we are not told the weight of the beam, so our answers will be in terms of $W$...

 

Question 10: In our 'model' of the situation, the two geezers would be two supports and the dead body would be a rigid beam (especially if rigor mortis has set in):

 

It makes sense to take moments about ‘C’ - That way, the unknown force $W$ is eliminated:

 
                    ◄─ Force through the PIVOT 
                        has ZERO moment - ignore!                      ◄─ A.C.W.M.
   
    Take Moments 
    about ‘A’ ──►
                                             
                                             
                     C.W.M ─►
 
└─────────┬─────────┘           AT EQUILIBRIUM:            └─────────┬─────────┘
│                                                          │
└──── CLOCKWISE MOMENTS    =   ANTICLOCKWISE MOMENTS ──────┘
(…) × (x)  =  (…)×(…-…)

 a jar is quite complicated - which means if you don't understand the mechanics, you'll never be able to open one and you'll probabily starve to death...

 

 

Question 12: It should be obvious, that the pivot will need to be placed a bit nearer end $B$ than end $A$; because the weight at $A$ is bigger, so the pivot needs to be closer to it to reduce the moment from that weight. So, our diagram looks like this:

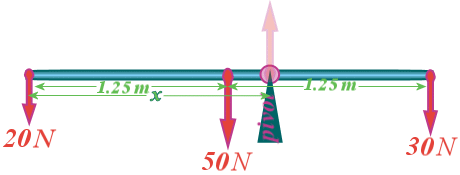
And, if we take moments  we can ignore the reaction force...

 

 

Question 13: The REAL-LIFE (life-or-death this case) situation looks like this:

                       Crazy-girl is risking her
                       life, "walking the plank" 
 
 
 
 
 
 
 
 
 
 
                                            ▲
                                            │
                                            └─┐
                                              └──┐
                                               when it does topple, this
                                               will be the PIVOT-POINT 
                                                              ┌─┘
                                                           ┌──┘
                                                       ┌───┘
                                                       │ this is where
                                                       ▼ she'll land!

Of course, we haven't shown any of the forces there (in the real world, you'll never see force arrows - but imagine how cool it would be if you did!)

NOTE that the edge of the roof is the pivot point, the point aornud which the plank will rotate when Hiral falls to her death! 

So here's our MODEL,with the forces shown: 

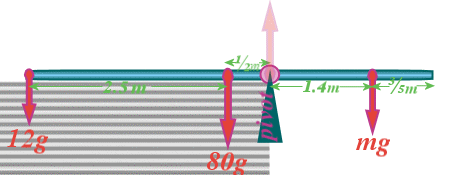
Then - it is easy!