Exercise 7E

Conservation of Vector Momentum

So, we know that momentum and impulse are vectors (Ex 7B), and we know that, in a collision, momentum is conserved (Ex 7D)...

...so, simply by applying conservation of momentum to cases where the momentum is given as a vector, we can understand questions involving conservation of vector momentum...

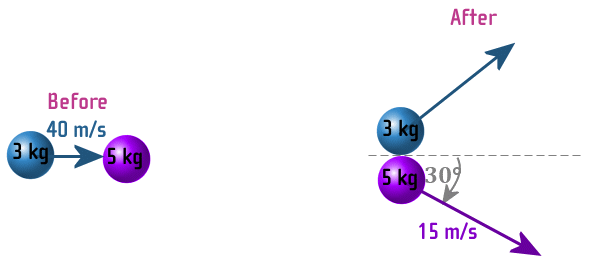
e.g. A 3 kg particle, travelling at 40 m/s due east, strikes a stationary body of mass 5 kg.
After the collision, the 5 kg particle moves on a bearing of 120°N at 15 m/s.
What is the speed of the 3 kg particle after the collision?

So, our before and after diagrams look like this:

We want to find the speed (which is a scalar) of the blue particle after the collision, but since we will start off by using vector momentum, I will show the Horizontal and Vertical components of the velocity of the blue particle:

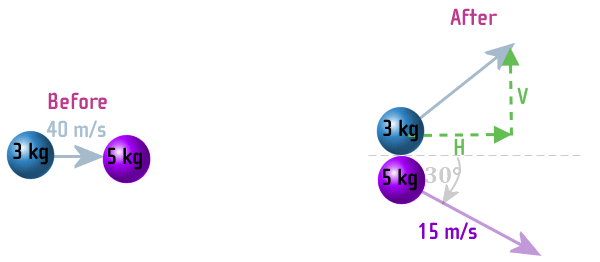
Then applying conservation of momentum separately along x (then along y):

CoM (along x): (3)(40) + (5)(0) = (3)(H) + (5)(15cos30)    ───────►  H = 18.35 m/s
	
CoM (along y):  (3)(0) + (0)(0) = (3)(V) + (5)(-15sin30)   ───────►  V = 12.5 m/s

So, we've worked out the vertical and horizontal components of the velocity of the blue blob, after the collision - bu they want the SPEED of the blue blob:

√18.35² + 12.5² = 22.2 m/s

Question 1: So, our before and after diagrams look like this:

Now, since are are going to be using vectors, let's find the horizontal and vertical components for the 600 m/s, but for the v, let's just write the horizontal and vertical components of v as H and V:

Then applying conservation of momentum separately along x (then along y):

CoM (along x):  (30)(0)  = (10)(600cos45) + (20)(-H)    ───────►  H = ... m/s
	
CoM (along y): (30)(400) = (10)(600sin45) + (20)(-V)    ───────►  V = ... m/s

So, we've worked out the vertical and horizontal components of the velocity of the black fragment, after the collision - but they want its SPEED:

√...² + ...² = ... m/s

Question 2: Let's imagine the 1.2 kg stone is sliding to the right at 16 m/s, and lets imagine that, after the collision, it is moving at 10 m/s at 60° above the x-axis...

We don't know which way the second particle moves after being hit, but I'd guess is moves to the right and below the x-axis - so lets give it a component of H (to the right( and a component of V (down):

Do a good sketch and then apply conservation of momentum separately along x (then along y):

CoM (along x): (1.2)(16) + (2)(0)  = (1.2)(10cos60) + (2)(H)    ───────►  H = ... m/s
	
CoM (along y):  (1.2)(0) + (2)(0)  = (1.2)(10sin45) + (2)(-V)    ───────►  V = ... m/s