Interactive Web Lesson
#21  ›  Functions 2
\(\require{cancel}\)

The Interactive Web-Lesson below has questions embedded
So do it carefully, as your answers are sent to me!

        
  • When a question pops up, if you want to see the movie again, click ‘Hide’ (top right corner)
  • You CAN'T retry a ‘flopped’ question: So PAY ATTENTION and THINK!
  • When you get a question ‘CORRECT’, you'll get an opportunity to ‘SKIP’ the explanation:
    Click the arrow in the right (but be quick!)
 
 
The Inverse of a Function: 
 
 

Functions II > The Inverse of a Function

A ‘transformation’ might be: ‘take a step forward’

In that case, the inverse transformation would be: ‘take a step backwards’

Why?

Because if you have already done the transformation (i.e. taken a step forwards), then doing the inverse transformation (i.e. taking a step backwards) would get you back to where you started...

So, if a transformation was: ‘turn clockwise by 90°’...
...then what would the inverse transformation be?

 

Not all transformations will have an inverse: For instance if the ‘transformation’ is ‘hit the nearest person’, well there's really no inverse is there?

 

One way to think of a function is to think of it as a ‘transformation’

For instance, if I put x=2 into the function: \(f\left( x \right) =10-2x\,\, \left\{ \,\,x: x\in \mathbb{R}, x\geqslant 0 \right\} \):

                                    f(2) = 10 - 2(2)
                                         = 10 - 4
                                         = 6

the answer is: ‘6’

So, we can say that the function transformed the input number ‘2’ into the output number ‘6’

                        input
                  ┌———————►—————————┐
                  │               ╔═╧═══════════════╗
                  2               ║   function: f   ║                       
                                  ╚═══════════════╤═╝               
                                                  └————————►————————┐
                                                        output      ▼
                                                                    6

The inverse function will undo the transformation:

                        input
                  ┌———————►—————————┐
                  │               ╔═╧═══════════════╗
                  2               ║   function: f   ║                       
                  ▲               ╚═══════════════╤═╝               
                  │                               └————————►————————┐
                  │                                     output      ▼
                  │                                                 6 
                  │                                                 │
                  │                               ┌————————◄————————┘
                  │               ╔═══════════════╧══╗
                  └———————◄———————╢ inverse function ║                       
                                  ╚══════════════════╝

If the function is called \(f\left( x \right) \), then its inverse is called: \(f^{-1}\left( x \right) \) 

 

Finding the Inverse Function:

  1. If possible, sketch the function an find its ‘range’ (this will become the ‘domain’ for the inverse function)
  2. Write the function as: y = . . . . . . (instead of f(x) = . . . . . .)
  3. Now make ‘x’ the subject of this equation
  4. Now change the ‘x’ to a ‘y’ and change every ‘y’ to an ‘x’ (there might be more than ‘1’)
  5. This is the inverse function, but finally, instead of leaving it as y = . . . . . . we write it as f-1(x) = . . . . . .
  6. Now the range that you worked out in Step 1 will become the domain of your inverse function...

 

e.g. In the example above: \(f\left( x \right) =10-2x\,\, \left\{ \,\,x: x\in \mathbb{R}, x\geqslant 0 \right\} \). Find the inverse function, \(f^{-1}\left( x \right) \)

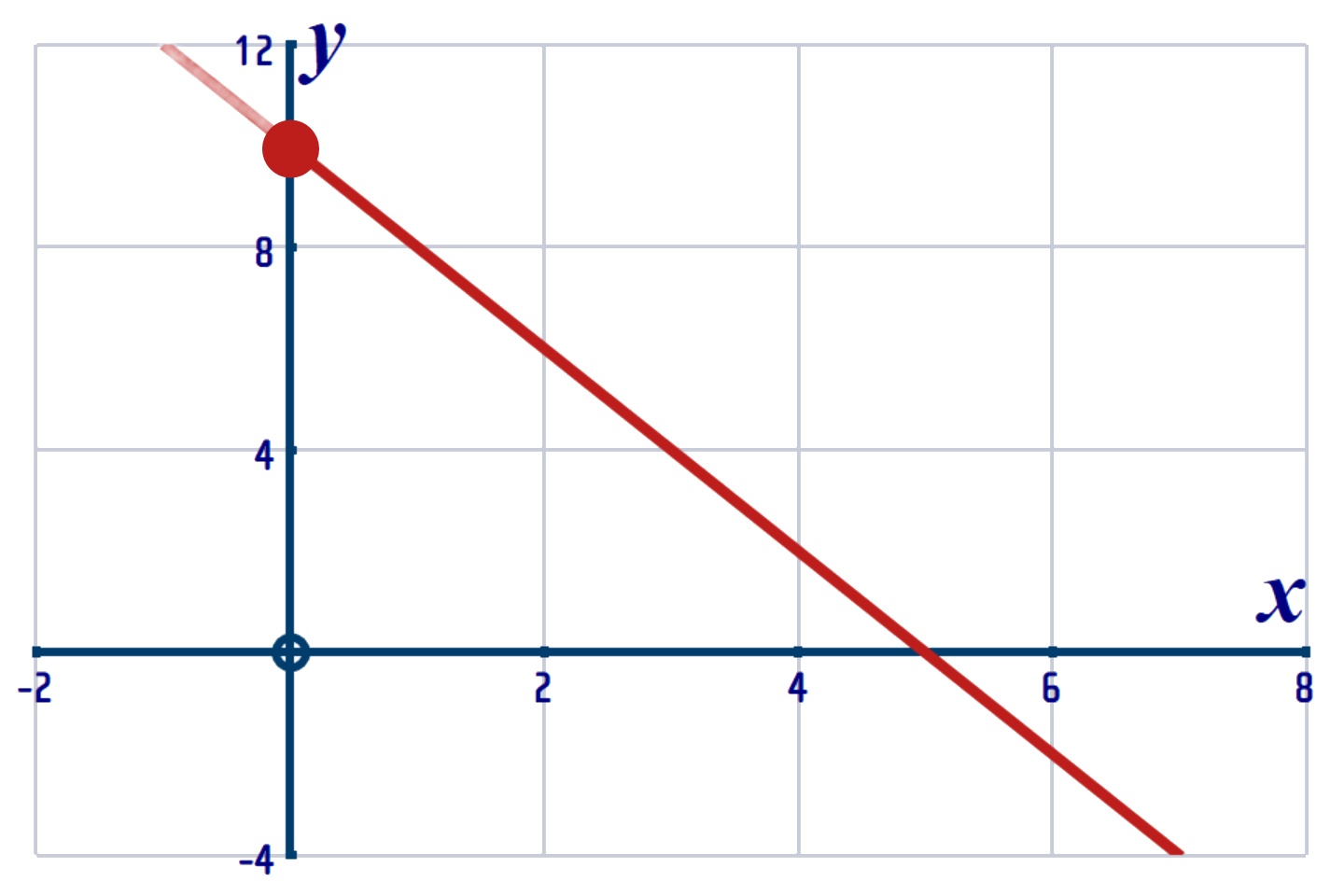
A quick sketch (this is just a straight line, so it's really easy to sketch) shows that (taking into account the ‘DOMAIN’) the graph looks like this:

We now know the range: \(\left\{ \,\,y: y\in \mathbb{R}, y\leqslant 0 \right\} \)

This will become the DOMAIN for our inverse function...

 
                                                                   ╔══════════╗
                                      f(x) =  10 - 2x  ◄———————————╢ function ║
                                                                   ╚══════════╝
Step 1: Write as y = ......             y  =  10 - 2x
                                    +2x          + 2x
Step 2: Now make ‘x’ the subject:   -----------------
                                    y + 2x =  10
                                   -y            - y
                                   -----------------
                                        2x =  10 - y
                                        χ2     χ2  χ2
                                        -------------
                                         x =  5 - ½y
                                         ↓         ↓
Step 3: Swap ‘x’s & ‘y’s:                y =  5 - ½x
 
Step 4: Write as f-1(x) = …:         f-1(x) =  5 - ½x
                                                                      
Step 5: Old DOMAIN becomes:          f-1(x) =  5 - ½x   { x: x x ∈ ℝ, x ≤ 10 }
        new RANGE                   └────────────┬────────────────────────────┘
                                                 │
                                       ╔═════════╧═════════╗
                                       ║  inverse function ║
                                       ╚═══════════════════╝

Now earlier, I told you that the inverse function undoes the transformation of the original function

And, we put x=2 into the original function { f(x) = 10 - 2x } and found the answer was '6'

So, if we put x=6 into the inverse function, it should take us back to the original number (x=2)

Lets check:

                        f-1(6) = 5 - ½(6)
 
                               = 5 - 3
 
                               = 2

See, it works!

·

·

Question 1: \(f\left( x \right) =4x+12 \left\{ \,\,x: x\in \mathbb{R} \right\} \). Define the inverse function,\(f^{-1}\left( x \right) \)

·

Clue:


We can find the equation of the inverse function:

                                 f(x) =  4x + 12
 
STEP 1: Write as y = ......        y  =  4x + 12
                                  -…        - …     ╒════════════════════╕
STEP 2: Now make x subject:    -----------------    │ It might help to   │
                               y - …… =  4x         │ use a flow diagram │
                               χ…  χ…    χ…         │ when re-arranging  │
                              -------------         ╘════════════════════╛
                              Όy - …… =   x
                               ↓          ↓
STEP 3: Swap ‘x’s & ‘y’s:     Όx - …… =   y
                                         └┬┘
STEP 4: Write as f-1(x) = …:  Όx - …… = f-1(x)
  
So, the answer is:             f-1(x) =  Όx - ……    { x: x ∈ ℝ }
                              └────────────┬─────────────────────┘
                                           │
                                 ╔═════════╧═════════╗
                                 ║  inverse function ║
                                 ╚═══════════════════╝
        

·

·

Question 2: \(g\left( x \right) =4\left( x+3 \right) , \left\{ \,\,x: x\in \mathbb{R} \,\, \right\} \)
Define the inverse function \(g^{-1}\left( x \right) \)
        
Clue: 
 
Start by writing as y = ......           y  =  4(x + 3)
 
Now, we need to make ‘x’ the subject. It helps to use a flow diagram:
 
    x                                    y  =  4(x + 3) 
    │
    ▼
   +3
    │
    ▼
   Χ4
    │
    ╘═════╛
      = y
 
To make ‘x’ the subject, we need to reverse the steps:
 
The opposite of ‘Χ4’ is ‘χ4’:
 
    x                                    y  =  4(x + 3) 
    │                                   χ4    χ4
    ▼                                   --------------
   +3                                   Όy  =    x + 3
    │
    ▼
   Χ4     χ4
    │     ▲
    ╘═════╛
      = y
 
The opposite of ‘+3’ is ‘-3’:
 
    x                                    y  =  4(x + 3) 
    │                                   χ4    χ4
    ▼                                   --------------
   +3     -3                            Όy  =    x + 3
    │     ▲                              -3        - 3
    ▼     │                          -----------------
   Χ4     χ4                         Όy - … =    x
    │     ▲
    ╘═════╛
      = y
 
So, the final step is to write it as: f-1(x) = ...... 
        

·

·

Question 3: \(h\left( x \right) \,=\,\frac{7}{x-5}, \left\{ \,x: x\in \mathbb{R} , x\ne 5 \right\} \). Find \(h^{-1}\left( x \right) \)

·

Clue: 
 
Use the same method as above…
 
When making ‘x’ the subject, it helps to use a flow diagram:
 
    x                                    y  =    7    
    │                                          x – 5  
    ▼
   –5
    │
    ▼
  RECIP ◄—————————— 'RECIP' of (x–5) means: Ή⁄₍ₓ₋₅₎
    │
    ▼
   χ7
    │     ▲ 
    ╘═════╛
      = y
        

·

·

Question 4: \(j\left( x \right) =4 -\,\,\frac{3}{2-x}, \left\{ \,\,x: x\in \mathbb{R} , x\ne 2 \right\} \)
a) Find \(j^{-1}\left( x \right) \)
b) Find \(j^{-1}\left( 2 \right) \)
Clue: 
 
Use the same method as above…
 
When making ‘x’ the subject, it helps to use a flow diagram:
 
    x                            y  =  4  -    3    
    │                                        2 - x 
    ▼
   Χ-1
    │
    ▼
   +…
    │
    ▼
  RECIP
    │
    ▼
   χ…
    │
    ▼
   Χ-1
    │
    ▼
   +…
    │     ▲
    ╘═════╛
      = y
        
Once you've finished, remember there's an AUTOMATIC RESTRICTION to the domain that applies
for this type of equation!
 
 
Next, they want us to find: f-1(2), which means we have to:
                            ▲   ▲
                            ║   ╚═══ put x = 2
                            ╚══════ into the inverse function
 

 
Note: We can check to see if our answer is right by putting it back into the original function:
 
                 input
          ┌———————►—————————┐
          │               ╔═╧═══════════════╗
         ...              ║   function: f   ║                      
          ▲               ╚═══════════════╤═╝               
          │                               └————————►————————┐
          │                                     output      ▼
          │                                                1/2 
          │                                                 │
          │                               ┌————————◄————————┘
          │               ╔═══════════════╧══╗
          └———————◄———————╢ inverse function ║                      
                          ╚══════════════════╝               
 
So, when we put x = ... into the original function, it should give: ‘1/2’
        

·

·

Question 5: \(f\left( x \right) =\,\,\frac{1}{x+2}\,\, \left\{ \,\,x: x\in \mathbb{R}, x\ne 2 \right\} \). Find \(f^{-1}\left( \frac{2}{5} \right) \)

·

Clue: 
 
They want us to find: f-1(2/5), which means we have to:
                      ▲   ▲
                      │   └─── put x = 2/5
                      └─────── into the inverse function
 
They don't REALLY ask us to DEFINE the inverse function - so we can skip the normal steps!
 
We'll skip straight to the step where we find the EQUATION of the inverse function:
 
                                          f(x)	=    1 
                                                   x + 2 
 
STEP 1: Write as y = ......                y  	=    1 
                                                   x + 2 
                                         RECIP   RECIP
STEP 2: Now make ‘x’ the subject:     --------------------
                                      1/y     	=  x + 2
                                           -2         -2
                                      ------------------  
                                      1/y - ……	=  x
                                            ↓      ↓
STEP 3: Swap ‘x’s & ‘y’s:             1/x - ……	=  y
 
STEP 4: Write as f-1(x) = .....        1/x - ……	= f-1(x)
  
Once you've finished, remember there's an AUTOMATIC RESTRICTION to the domain that applies
for this type of equation!
 
 
Now we've found the inverse function, we can go ahead and find f-1(2/5)
 
The inverse function is:               f-1(x)  	=  1/x  -  ……
 
                                       f-1(2/5)	=   1   -  ……
                                                  (2/5)
 
                                              	=  2.5  -  ……
 
                                              	=     ... 
 
Note: We can check to see if our answer is right by putting it back into the original function:
 
                  input
            ┌———————►—————————┐
            │               ╔═╧═══════════════╗
           ...              ║   function: f   ║                       
            ▲               ╚═══════════════╤═╝               
            │                               └————————►————————┐
            │                                     output      ▼
            │                                                2/5 
            │                                                 │
            │                               ┌————————◄————————┘
            │               ╔═══════════════╧══╗
            └———————◄———————╢ inverse function ║                       
                            ╚══════════════════╝               
 
So, when we put x = ... into the original function, it should give: ‘2/5’

·

·

Question6: \(f\left( x \right) =\frac{10}{x\,\,+\,\,2}\,\,\left\{ \,\,x: x\in \mathbb{R} , x\geqslant -10 \right\} \)
Find \(f^{-1}\left( -\frac{1}{2} \right) \)

·

Clue:
 
To find the inverse function, start with a flow diagram (which starts with ‘x’):
 
 
     x                                y  =     10    
     │                                       x + 2  
     ▼
    +2
     │
     ▼ 
   RECIP ◄—————————— ‘RECIP’ing (x+2) turns it into:    1
     │                                               (x + 2) 
     ▼
    Χ10
     │
     ▼     ▲
     ╘═════╛
       = y
      
Once you've finished, remember there's an AUTOMATIC RESTRICTION to the domain that applies
for this type of equation!

BUT, there'll also be a further restriction to the domain - because the ORIGINAL function
had its domain cut-back; but we don't know how to deal with that - so let's not worry
about it too much (after all, they don't actually ask us to define the inverse function…)
 
Still, it can't hurt to be AWARE!

·

·

Question 7: \(f\left( x \right) =\,\sqrt{16-2x}\,\left\{ \,x: x\in \mathbb{R} , x\leqslant 8\, \right\} \)
a) Find \(f^{-1}\left( 4 \right) \)
b) Hence sketch the original function, \(f\left( x \right) \)

·

Clue: 
 
First, find the inverse function f-1(x),then put x=4 into this inverse function:
 
 
                                            f(x)	= √16-2x 

STEP 1: Write as y = ......                   y 	=  √16 - 2x
                                            SQR     SQR
STEP 2: Now make ‘x’ the subject:           ----------------
                                             …… 	=   16 - 2x
                                              -16     -16
                                            ----------------
                                           …… - …	=   -2x
                                           χ-2 χ-2     χ-2
                                           ---------------    
                                           …… + 8	=     x 
                                            ↓            ↓
STEP 3: Swap the ‘x’s & ‘y’s:              …… + 8	=     y
 
STEP 4: Write as f-1(x) = ......            …… + 8	=  f-1(x)
 
Now, putting in x=4 into this inverse function to find f-1(4):
  
The inverse function is:                    f-1(x)	= -………  +  …
 
                                            f-1(4)	= -(4)² + …
                                                     2   . 
 
                                                 	= -……  + …
 
                                                 	=   ...
 
Note: We can check to see if our answer is right by putting it back into the original function:
 
                   input
            ┌———————►—————————┐
            │               ╔═╧═══════════════╗
           ...              ║   function: f   ║                       
            ▲               ╚═══════════════╤═╝               
            │                               └————————►————————┐
            │                                     output      ▼
            │                                                 4 
            │                                                 │
            │                               ┌————————◄————————┘
            │               ╔═══════════════╧══╗
            └———————◄———————╢ inverse function ║                       
                            ╚══════════════════╝               
 
So, when we put x = … into the original function, it should give: ‘4’
 
Part (b):
 
How do they expect us to sketch  f(x) = √16-2x ???
 
But hold on - the INVERSE FUNCTION is just a quadratic - we can easily sketch that…
 
Once we've done that, there's a simple trick to convert that into a sketch
of the original function

                 ┌›─›─›─›─›─›─›─SWIZZLE-THE-PAGE─›─›─›─›─›─›─›┐ 
        ╒════════╧═══════╕                           ╒════════╧═════════╕
        │ SKETCH of f(x) │                           │ SKETCH of f⁻Ή(x)	│
        ╘════════╤═══════╛                           ╘════════╤═════════╛
                 └‹─‹─‹─‹─‹─‹─‹─SWIZZLE-THE-PAGE─‹─‹─‹─‹─‹─‹─‹┘

Sketching the INVERSE of a FUNCTION

If we can draw \(f\left( x \right) \), then drawing \(f^{-1}\left( x \right) \) is super simple!

Similarly, if we can draw \(f^{-1}\left( x \right) \). then converting that to a drawing of \(f\left( x \right) \) is easy!

In this case, we can't draw \(f\left( x \right) \), BUT, \(f^{-1}\left( x \right) \) is just a QUADRATIC, that we can draw with ease:

Once you've drawn it, trace the curve again - with a thick pen! (the nib size of the pen, not it's intelligence) i.e. a Sharpie

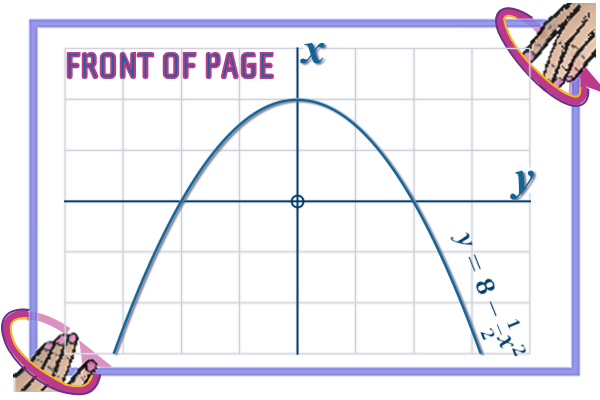
(Why did I draw it with the \(x\) and \(y\) axes the wrong way around??? Well, that's one way of thinking about what inverting a function really is! It is just swapping the \(x\) and \(y\) (the rest is just re-arranging and notation... And this sketch was of the inverse of the original function)

Now, hold the bottom left corner of the page with one hand, and the top right corner of the page with the other (as shown above) ; then SWIZZLE the page so that you are looking at the graph from the back of the page…

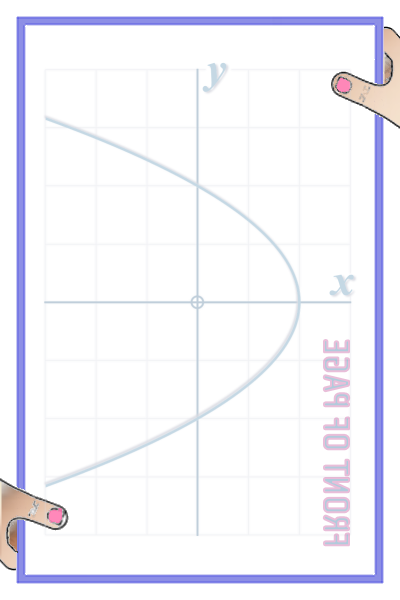
That's the inverse function (you should notice that, doing this, we've now SWAPPED the \(x\) and \(y\) axes back!):

If you can't see it, it means you didn't use a thick enough pen. Try holding the page up to the light!

·

That's ALL nice and clear and easy and enjoyable to follow - but there is a problem with the graph that we've ended up with: The problem is that \(\sqrt{x}\) is NEVER-NEGATIVE. (By definition, \(\sqrt{\;\;\;}\) means the POSITIVE-ROOT, so \(\sqrt{9}\,\,=\,\,3\) and is NOT \(\pm 3\) - that's why, when we learnt algebra, we learnt  that actually the OPPOSITE of  \(\boxed {\,SQR\,}\) is: \(\boxed {\,\pm \sqrt{\;\;\;}\,}\)...)

Anyways - back to what I was saying before I starting ranting; The problem is that \(\sqrt{x}\) is NEVER-NEGATIVE - so how does our graph of \(y=\sqrt{16-2x}\) give a whole load of negative \(y\)-values???

The answer is - it shouldn't... So you is gotchta delete half of the curve above...

(I wonder if you could drill back into the working that we did in STEP 2 to identify WHEN THIS ERROR crept in???)
 

·

·

Question 8: \(p\left( x \right) =5 -\,\,\sqrt{x-3}, \left\{ \,\,x: x\in \mathbb{R} , x\geqslant 3 \right\} \)
Define \(p^{-1}\left( x \right) \)
Hence sketch the ORIGINAL function, \(p\left( x \right) \)
Clue: Use the same method as in the last few questions…
        

·

·

Question 9: \(y\left( x \right) =\frac{x}{x-2}, \left\{ \,\,x: x\in \mathbb{R} , x\ne 2 \right\} \). Find \(y^{-1}\left( x \right) \)

·

Clue: 
 
Start by writing as y = .....            y  =    x
                                               x - 2 
 
Now, we need to make ‘x’ the subject of this - and since ‘x’ is in two places, we use the 6 step
programme for re-arranging:
 
Step 1: Brackets:                        y  =    x
                                              (x - 2) 
                                   Χ(x - 2)  Χ(x - 2)
Step 2: Multiply by denominator:   ------------------
                                   y(x - 2) =   x
 
Step 3: Multiply out brackets:     …  -  …  =   x
                                   -…             - …
Step 4: Collect ‘x’ terms:        ------------------
                                         …  =  x - …
 
Step 5: Factorise ‘x’ out:               …  =  x(1 - …)
 
Step 6: Divide to make ‘x’ the subject:
 
Finally, we need to write this as f-1(x) = .......

·

·

Question 10: \(f\left( x \right) =\frac{2-x}{1+x}, \left\{ \,\,x: x\in \mathbb{R} , x\ne -1 \right\} \)
Define fully, the inverse function. Hence find \(f^{-1}\left( -\frac{1}{2} \right) \)
Clue: Use exactly the same method as above…

Complete this web lesson on separate paper from any other homework

The pass mark (to avoid additional homework on this topic) is:  8/10 

Show FULL workings and highlight your answers

.