|
Web Lesson: Statistics
#11 › Cumulative Frequency Curves
The Interactive Web-Lesson below has questions embedded
|
x |
5-15 |
15-20 |
20-23 |
23-26 |
26-29 |
29-33 |
33-38 |
|
f |
13 |
18 |
35 |
42 |
34 |
13 |
5 |
Represent these data using an Ogive:
- Write a new table out, with the first row representing the upper boundary of each class (but start it with the L.C.B. of the 1st class)
U.C.B.
up to 5
up to 15
up to 20
up to 23
up to 26
up to 29
up to 33
up to 38
- Along the second row, write the cumulative frequencies (called ‘F’):
U.C.B.
up to 5
up to 15
up to 20
up to 10
up to 15
up to 20
up to 25
up to 30
F
0
13
31
66
108
142
155
16
▲ ▲ ▲ ▲ ▲ ▲ ▲ ┐└─┐ │ │ │ ╚════════etc═════════╝ Use L.C.B. of │ │ │ │ │ the 1st class ├──┘ │ │ │ and F = 0 │ ┌────┴───┐ │ │ ┘ 1st freq │ │ │ │ ┌───────┴───────┐ │ 1st + 2nd freqs │ 13 + 18 = 31 │ │ ┌──────────┴──────────┐ 1st + 2nd + 3rd freqs 13 + 18 + 35 = 66 - Now draw your Ogive, plotting the points, with the ‘cumulative frequencies’ on the y-axis and the upper class boundaries on the x-axis:
- Connect these points with a smooth curve that starts from the origin and ends with a flat (horizontal) line after the last point:}
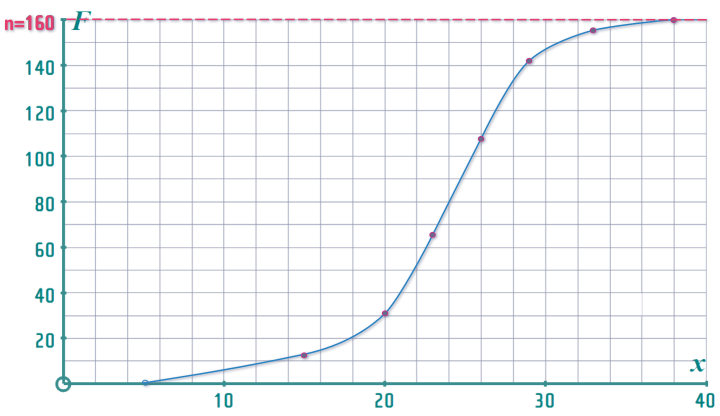
- The FINAL-VALUE in your cumulative frequencies is \(n\) (the sample-size) - you should always show this on the Cumulative Frequency Curve (as a dashed horizontal line)
As you complete this Web Lesson, you see links for the grids that you need to print off and utilise to help you to answer the question...
Alternatively, click HERE to download all of the links in 1 go!
Question 1: A class of 60 pupils were asked how much Christmas money they received
The results are given in this table:
Amount (£) |
5-20 |
20-30 |
30-40 |
40-50 |
50-70 |
70-120 |
|
Number of pupils |
8 |
15 |
18 |
11 |
6 |
2 |
a) Complete the following cumulative frequency table for these data:
U.C.B. |
up to 5 |
up to 20 |
up to ⋯ |
up to ⋯ |
up to ⋯ |
up to ⋯ |
up to 120 |
Cumulative Frequency |
0 |
8 |
⋯ |
⋯ |
⋯ |
⋯ |
60 |
b) Using the GRID linked here, sketch the Cumulative Frequency Curve for these data
CLARIFICATION: In this web lesson, you see classes written in the form \(5-20\) ...
...which is just an abbreviated way of saying: \(5\leqslant x<20\)
Hints:
Step 1: Always CHECK the data is written using CLASS BOUNDARIES (not class-limits) ✔ IT IS
(i.e. there no GAP between the end of any class and the start of the next class)
Step 2: To populate the TOP-ROW of the Cumulative Frequency Table, look at the LIMITS of each class:
The first class is SPECIAL: ‘5 - 20’
▲ ▲
│ │
This is the only class where its L.C.B. ─────┘ │
ISN'T deleted: its the 1st № in our CF │
table (the F-value below it is just ‘0’) └────────── This is the 2nd № in the
top-row of our CF-table
After that, fill in the U.C.B.s of the rest of classes to complete the top-row:
Step 3: To populate the BOTTOM-ROW, you need to work out the ‘running-totals’ of the frequency
┌───┐
We saw already that the first number in the F-row is: |‘0’|
After that - the values are: 8 = | 8 |
8 + 15 = | ⋯ |
8 + 15 + 18 = | ⋯ |
8 + 15 + 18 + …… = | ⋯ |
8 + …… + …… + …… + … = | ⋯ |
8 + …… + …… + …… + … + … = | ⋯ |
└─┬─┘
these are our CUMULATIVE FREQUENCIES ───────┘
Step 4: PRINT off the grid provided (see the link in the question), plot the points
and connect them with a smooth curve (smooth out the curve, even if it means you slightly
miss one of your points
Question 2: Some data was collected on the time taken to complete a crossword (with a 2-minute penalty for each incomplete/incorrect entry:
Time (mins) |
10-15 |
15-30 |
30-40 |
40-50 |
50-65 |
65-90 |
|
Frequency |
4 |
25 |
36 |
27 |
7 |
1 |
a) Form a cumulative frequency table for these data
b) Using the GRID linked here, sketch the Cumulative Frequency Curve for these data
Hints:
Step 1: Always CHECK the data is written using CLASS BOUNDARIES (not class-limits) ✔ IT IS
(i.e. there no GAP between the end of any class and the start of the next class)
Step 2: To populate the TOP-ROW of the Cumulative Frequency Table, look at the LIMITS of each class:
The first class is SPECIAL: ‘10 - 20’
▲ ▲
│ │
This is the only class where its L.C.B. ─────┘ │
ISN'T deleted: its the 1st № in our CF │
table (the F-value below it is just ‘0’) └────────── This is the 2nd № in the
top-row of our CF-table
After that, fill in the U.C.B.s of the rest of classes to complete the top-row
TIME (UCB) │ 10 15 30 40 50 65 90
───────────┼───────────────────────────────────────────────────────
F │ 0 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯
Step 3: To populate the BOTTOM-ROW, you need to work out the ‘running-totals’ of the frequency
Step 4: PRINT off the grid provided (see the link in the question), plot the points
and connect them with a smooth curve (smooth out the curve, even if it means you slightly
miss one of your points
Question 3: Indian airlines tells its passengers that they can "carry on" hand baggage of up to 10 kg, but anything above 10 kg has to be checked into the hold and the customer needs to PAY for it.
On Tuesday's flight, 48 people tried to board the plane with OVERWEIGHT hand-baggage". This table summarises the masses of those idiots:
Mass (kg) |
10-16 |
16-19 |
19-22 |
22-26 |
26-40 |
|
frequency |
4 |
14 |
18 |
9 |
3 |
a) Complete a Cumulative Frequency table for these data
b) Using the GRID linked here, sketch the Cumulative Frequency Curve for these data
Hints: Don't start your cumulative frequency curve from the point (0, 0) As we have done in the questions so far, this time, you have to start from the point (10, 0)
Analysing a Cumulative Frequency Curve
Referring back to our data on the distance the Javelin was thrown by a sample of students
x |
5-15 |
15-20 |
20-23 |
23-26 |
26-29 |
29-33 |
33-38 |
|
f |
13 |
18 |
35 |
42 |
34 |
13 |
5 |
- When you put in an x-value and read across, the answer to the corresponding y-value (say ‘x=22’):
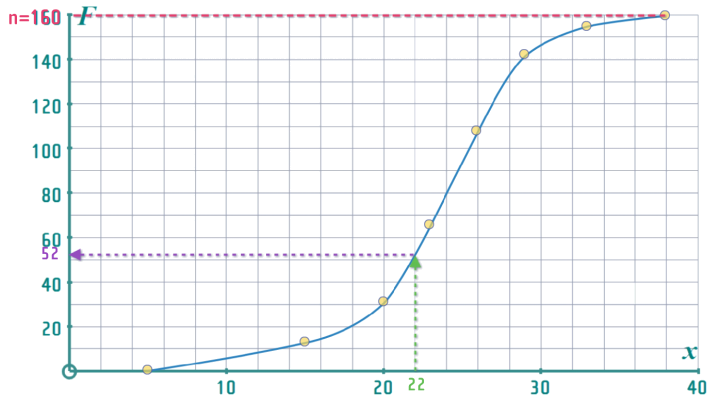
- The answer (y=52) tells you "how many students got LESS THAN than ‘22’:
Note: The number on the y-axis is always the answer to the question, "how many got LESS THAN x=..."
- To find how many students achieved a throw of greater than 22m, simply compute \(n\) - y-value (i.e. 160-52 = 138)
- To find the MEDIAN and quartiles, simply compute \(\frac{1}{2}n\) (or \(\frac{1}{4}n\) for Q1, or \(\frac{3}{4}n\) for Q3) and then insert that as a \(y\)-value using the cumulative frequency curve to find the corresponding \(x\)-value(s):
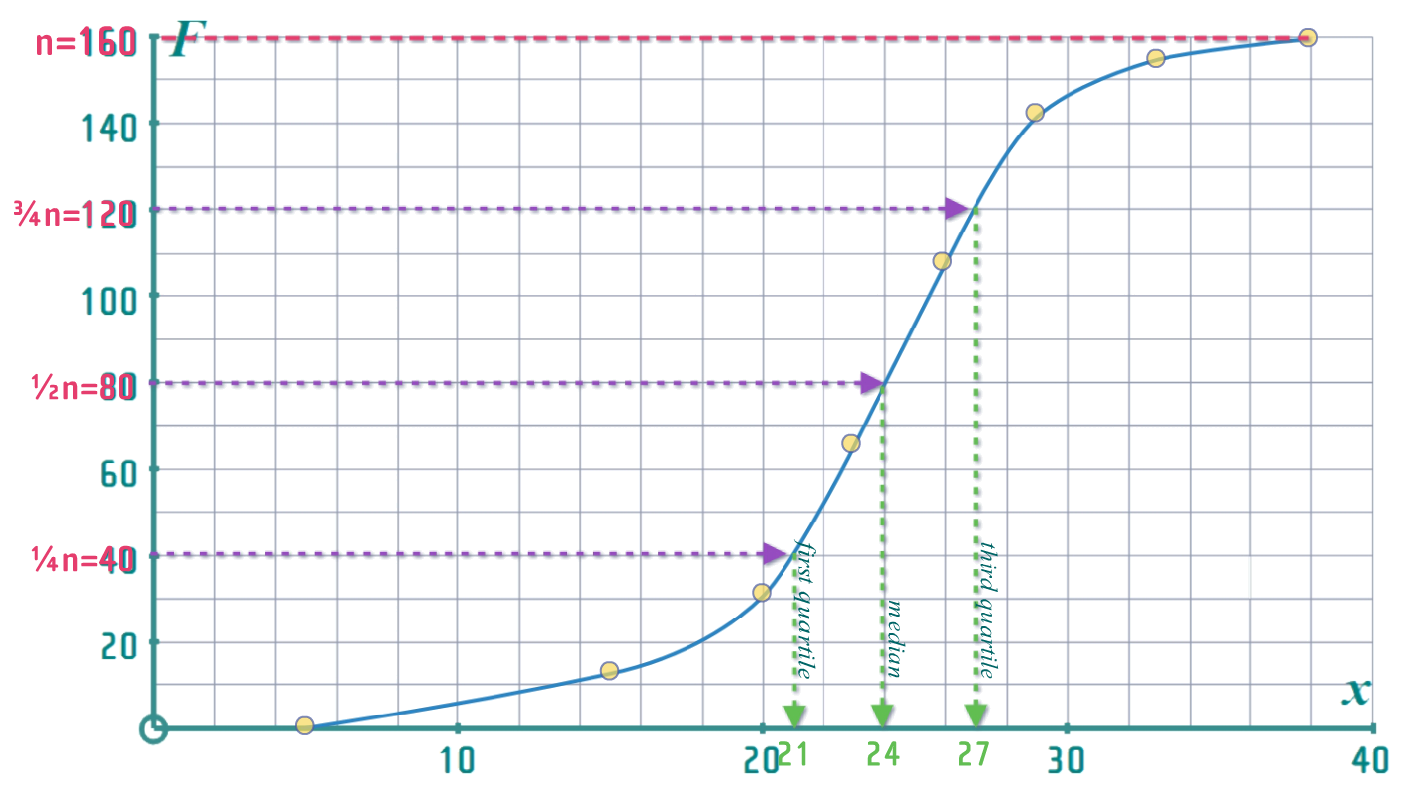
Note: Strictly speaking, if \(\color{#e54239}{n=100}\), then the middle value is the \(\left( \frac{1}{2}\color{#e54239}{100}+\frac{1}{2} \right) ^{th}\) value (i.e. the 50½th value) - so we should really have looked up 50½ on the y-axis - but in practice, when \(\color{#e54239}{n}\) is large (bigger than 30) then the difference between using \(\left(\frac{1}{2} \color{#e54239}{n}+\frac{1}{2} \right) \) and just \(\frac{1}{2}\color{#e54239}{n}\) isn't really worth bothering with; so - by convention - we only use \(\left(\frac{1}{2} \color{#e54239}{n}+\frac{1}{2} \right) \) when \(\color{#e54239}{n}\leqslant 30\)...
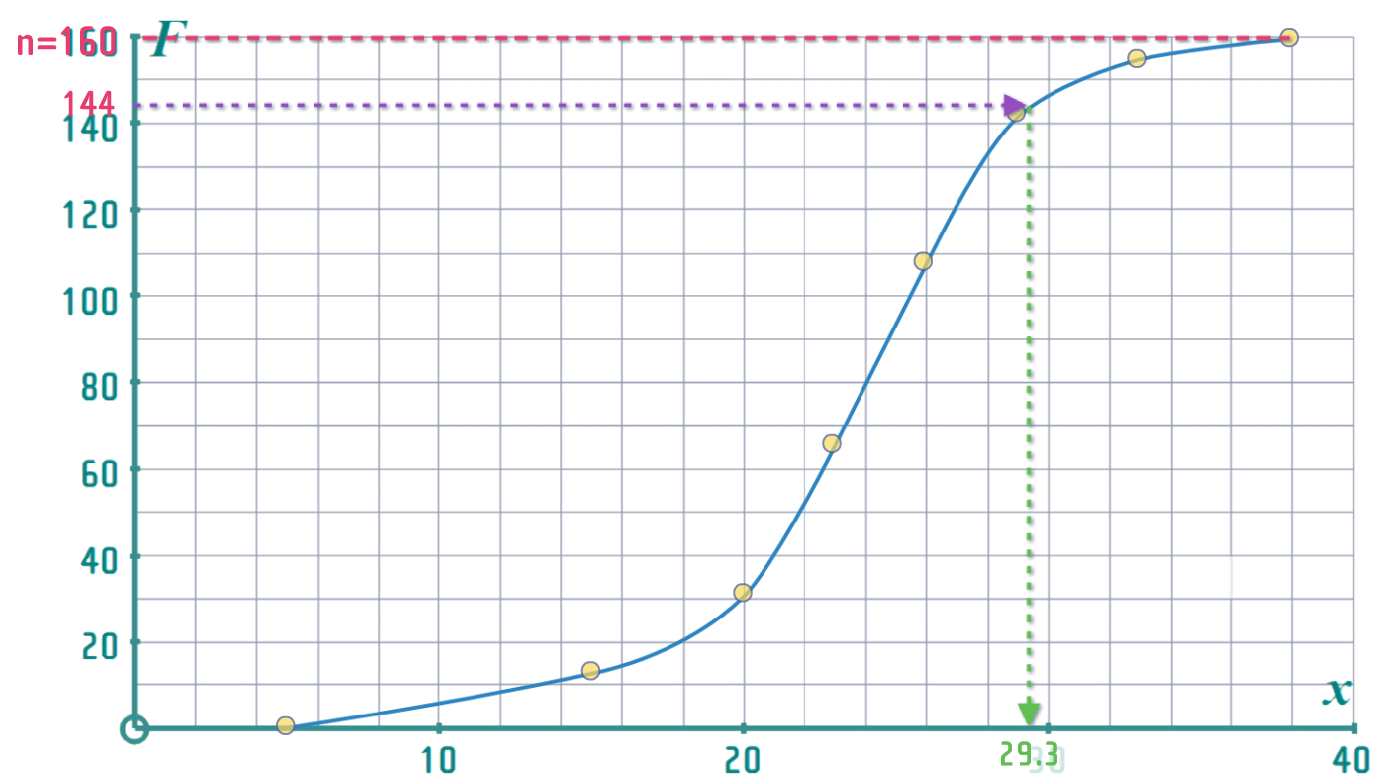
- Percentiles are just like quartiles (except there are more of them... ?): To find the 90th Percentile, compute \(\frac{90}{100}n\), and then insert that as a \(y\)-value using the cumulative frequency curve to find the corresponding \(x\)-value:
Question 4: The Southern Rail Service's 8:15 train to Paddington has been experiencing large delays over the past 3 months.
A survey was taken last month of the amount of time commuters spent waiting for the 8:15 train and the results are summarised in the Cumulative Frequency Curve below (you can download it here)
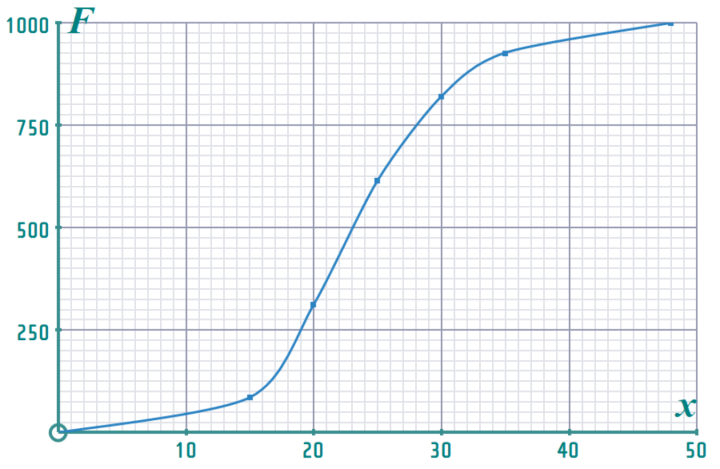
a) From your printout of the curve, estimate* how many of the 1000 commuters surveyed waited less than 30 minutes for their train
The train company must refund any commuter who has to wait 30+ minutes for the train
b) Estimate* how many commuters can apply for a refund?
The regulator will FINE the company £2,000,000 if 2% (or more) of commuters experienced 'excessive' delays ('excessive' is defined as: 45 minutes or more), raising the fine to £5,000,000 if 5% (or more) experienced excessive delays
c) How much (£0 if you decide 'NO FINE') will the company be fined?
*Marks will only awarded if your answer is accurate to ±5% - Print the graph off and be as accurate as you can
Hints: Part (a): Firstly - PRINT OFF THE FULL PAGE CUMULATIVE FREQUENCY CURVE for this question… We want to know how many people waited LESS THAN 30 minutes So, we go to "30" on the x-axis Add in a vertical line up to meet the curve and then a horizontal line across to the y-axis Reading the number from the y-axis tell us how many people waited less than 30 minutes Part (b): When we read a y-value from the GRID, it always tells us the NUMBER that were LESS THAN the corresponding x-value… If we wanna know how many were MORE than that x-value, we need to subtract the y-value from ‘n’ (remember, ‘n’ is the total number in the sample, which is the LAST number in the cumulative frequencies and also the y-value of the TOP of the ogive…)
Question 5: West Coast Railways wish to take over Southern's service - but their own train service to Hogsmeade Station has also suffered some delays. A much smaller sample gave these results:

a) From your printout of the curve, estimate* what percentage of these commuters waited 15-30 minutes for their train?
b) Estimate* how many of the 400 commuters surveyed waited 30+ minutes for their train. Comment on whether - based upon this criterion - West Coast Railways would be better at operating the service to Paddington, or not?
The regulator will also consider the number of excessive delays, before deciding if Southern should be stripped of the franchise...
c) Compare the data on excessive delays between the two companies: Which company looks better on this metric?
*Marks will only awarded for accuracy ±5% - print the graph off and be as accurate as you can
Hints: Part (a): If we draw a vertical line at x = 30 minutes and read across to the y-value - that will tell us how many passengers waited LESS THAN 30 minutes If we draw a vertical line at x = 15 minutes and read across to the y-value - that will tell us how many passengers waited LESS THAN 15 minutes SUBTRACT these two values, and we'll get the number that waited BETWEEN 15-30 mins How do we then turn that into a percentage? Part (b): Since the SAMPLE-SIZES are different, it's wrong to just compare the NUMBER that waited 30+ mins It makes much more sense to compare the PERCENTAGE that waited 30+ minutes Part (c): Again, we just need to compare the PERCENTAGES!
Question 6: The Cumulative Frequency Curve below summarises the data for the heights of 4000 G.C.S.E. students

Print off this cumulative frequency curve and estimate*:
a) the percentage of students were between 1.4m and 1.7m tall
b) how many students were exactly 1.5 m tall?
c) the height that the tallest 10% of students exceeded
d) the height that the shortest 25% of students were below
*Marks will only awarded if your answer is ±5% of the exact value. So, print the graph to show your workings and try to be as accurate as you can
Hints:
Part (a):
Start by finding the NUMBER of students that were 1.4 - 1.7 m tall: By drawing vertical lines
at x=1.7 and x=1.4, reading across to the y-values and subtracting…
Then turn it into a percentage (by dividing by 4000)
Part (b):
This is kinda a ‘trick’ question - but understanding the answer is gonna be crucial to your
understanding of continuous data…
It's not impossible to deduce: If you follow the logic of how you answered Part (a),
then it's kind-o-bvious - a ‘prize’ to anyone that gets it right!
Part (c): The TALLEST 10% refers to the 10% at the TOP of the curve…
…10% of 4000 is 400
└─────────┬─────────┘
│
└──────────────────── The 400 at the ‘TOP’ of the curve are
the 400 between y = 3600 and y = 4000
Question 7: Referring back to the data from QUESTION 1:
A class of 60 pupils were asked how much Christmas money they received
The results are given in this table:
Amount (£) |
5-20 |
20-30 |
30-40 |
40-50 |
50-70 |
70-120 |
|
Number of pupils |
8 |
15 |
18 |
11 |
6 |
2 |
Find the median and the interquartile range for these data
Hints: We already know that n = 60 (i.e. the total number in the sample was 60) The MEDIAN is the 30th value:
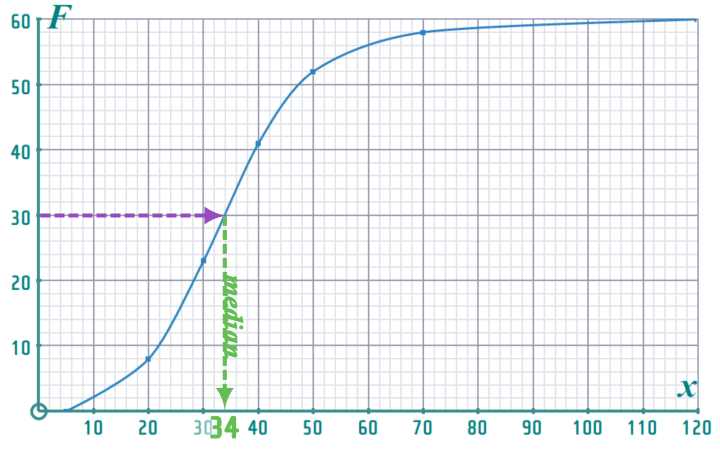
WARNING: ››› Students sometimes write: MEDIAN = 30 = 34 ‹‹‹ which you should obviously recognise gobbledegook (how and 30=34 ???) - it is BETTER to write: MEDIAN (30th value) = 34
Similarly, the 3rd QUARTILE is the 45th value, and the 1st QUARTILE is the 15th value
Question 8: Referring back to the data from QUESTION 2:
Some data was collected on the time taken to complete a crossword (with a 2-minute penalty for each incomplete/incorrect entry):
Time (mins) |
10-15 |
15-30 |
30-40 |
40-50 |
50-65 |
65-90 |
|
Frequency |
4 |
25 |
36 |
27 |
7 |
1 |
a) Estimate the median and interquartile range for these data
Barry and Sidoni are siblings and they are going to complete the crossword independently of each other
b) What is the probability the both of them complete it it under 28 minutes
Hints: Sorry - no help for you here!
Question 9: Referring back to the data from QUESTION 3:
Indian airlines tells its passengers that they can "carry on" hand baggage of up to 10 kg, but anything above 10 kg has to be checked into the hold and the customer needs to PAY for it.
On Tuesday's flight, 48 people tried to board the plane with OVERWEIGHT "carry-on baggage"
This table summarises the masses of those idiots:
Mass (kg) |
10-16 |
16-19 |
19-22 |
22-26 |
26-40 |
|
frequency |
4 |
14 |
18 |
9 |
3 |
When data is grouped like this - it is no longer possible to know the smallest and largest values from the original data: In that case, we use P10 (the 10th-PERCENTILE) and P90 (the 90th-PERCENTILE) as representing the extremes of the data
b) Estimate* P10 and P90 for these data
c) If two passengers are chosen at random, what is the chance that BOTH will be carrying bags weighing between P10 and P90?
*Marks will only awarded if accurate to ±5% of the exact value - be as accurate as you can
Hints: Firstly, before we can find median/quartiles etc we need a CUMULATIVE FREQUENCY TABLE and a CUMULATIVE FREQUENCY CURVE (remembering to show n = 48 on our curve) Americans call the MEDIAN the 50th percentile (we use: ½n, they use: ⁵⁰⁄₁₀₀n - same difference!) To find the 90th Percentile, start by working out ⁹⁰⁄₁₀₀n Then look up this value on the y-axis and read across to the x-axis
Question 10: Jack has wants to become 'hench'
He's started doing weights - but, because he's 'data focussed', he's been examining how much the other guys at the gym are able to bench-press. Here's his data:
Weight (kg) |
10-19 |
20-29 |
30-34 |
35-39 |
40-49 |
50-59 |
|
frequency |
7 |
21 |
28 |
32 |
23 |
9 |
a) Is this data written using 'CLASS-BOUNDARIES' or 'class-limits'?
b) Complete this cumulative frequency table
U.C.B. |
up to … |
up to … |
up to … |
up to … |
up to … |
up to … |
up to … |
F |
0 |
7 |
28 |
... |
... |
... |
120 |
c) Print off this grid and add the ogive to the grid
From your curve, estimate*:
d) How many gym-guys bench-pressed more than 45 kg
e) What is the median and what are the quartiles of the data
*Marks will only awarded if accurate to ±5% of the exact value - be as accurate as you can
Hints:
This is NOT WRITTEN using CLASS BOUNDARIES:
these should
be the same!
┌┬────────┬┐
▼▼ ▼▼
WEIGHT (kg) │ 10-19 20-29 30-34 35-39 40-49 50-59
─────────────┼─────────────────────────────────────────────────────────────────────────
f │ 7 21 28 32 23 9
The WEB LESSON showed you that, when that happens - you need to consider some values
between x = 19 and x = 20 and see which CLASS each value should be placed
┌─────────────┐ ┌─────────────┐
WHICH CLASS: │ 10 < x ≤ 19 │ OR │ 20 < x ≤ 29 │
┌┴────┬─┬─┬─┬──┘ ┌─┴───┬─┬─┬──┬──┴─┐
┌────┘ ┌───┘ │ │ └───┐ ┌────┘ ┌──┘ │ │ └──┐ └────┐
┌────┘ ┌────┘ ┌──┘ └──┐ └────┐ ┌─────┘ ┌─────┘ ┌──┘ └──┐ └────┐ └────┐
19 19.1 19.2 19.3 19.4 19.5 19.6 19.7 19.8 19.9 20
└─┬──┘
┌──┘
┌──────────────────────┴────┐
THIS IS THE CUT-OFF VALUE
└────┬──┬───────────────────┘
So we change: │ │
┌──┘ └──┐
WEIGHT (kg) │ ⋯-19.5 19.5-⋯ ⋯-⋯ ⋯-⋯ ⋯-⋯ ⋯-⋯
─────────────┼─────────────────────────────────────────────────────────────────────────
f │ 7 21 28 32 23 9
Next, do the same to ever UPPER-LIMIT (i.e. add ½)
Then, do the same to all the LOWER-LIMITS (i.e. subtract ½)
There - now we've got it written using CLASS-BOUNDARIES, we can carry on as usual!
NOTE: In this case, all UPPER-BOUNDARIES were increased by ½ and all LOWER-BOUNDARIES were decreased by ½: That's not ALWAYS the case:
One case where that rule doesn't apply is when x is the AGE of a person. Why? Because AGE is always rounded down (so a 19.8 year old person is still actually 19-years old, innit!)