Page 68, Column 2
Loci - Standard results:
Locus means "a path"
Often we constrain a point so it can only move according to
a rule. A simple way to understand this is is to think of our
point as being a train. It can only move along the tracks. So
the path taken by the train (i.e. the locus of the train) is the
line of the tracks
The plural of locus is loci
We can start to understand this topic by learning about some
standard results (i.e. situations that come up quite often)
1. Equidistant from a point
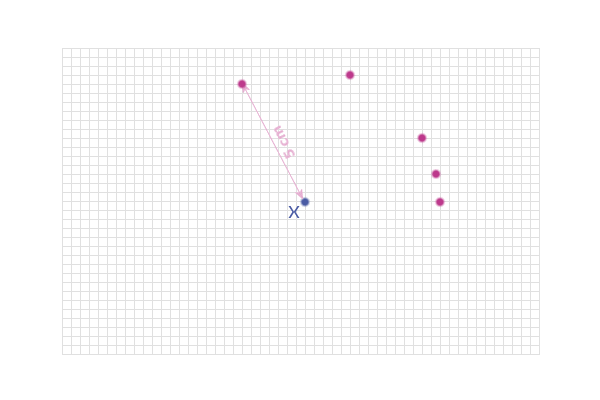
e.g. Find the locus of the points which are 5 cm from the
point X shown in the diagram below:

We can start by identifying any ONE POINT that obeys the rule
(i.e. is 5 cm from X):
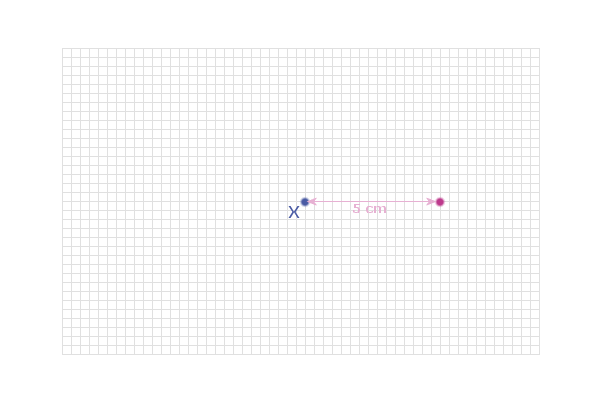
Then see if we can find another point that obeys the rule
(i.e. is also 5 cm from X):
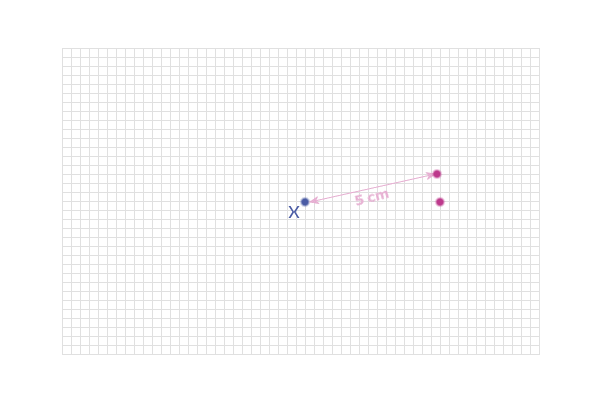
And another:
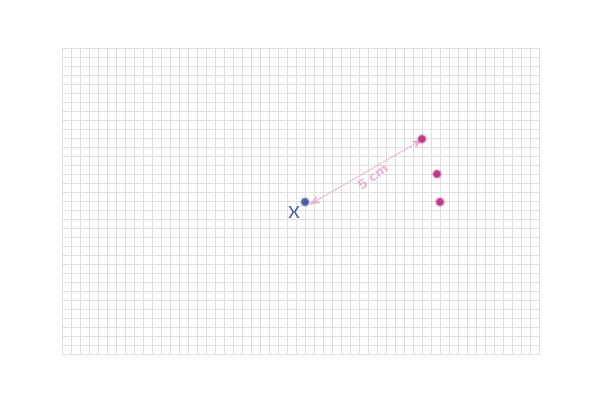
And another:
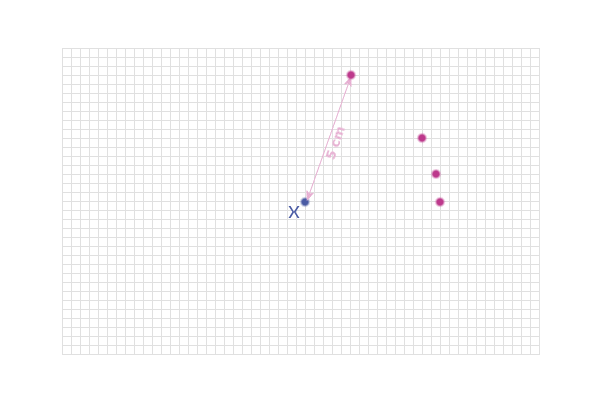
Etc...
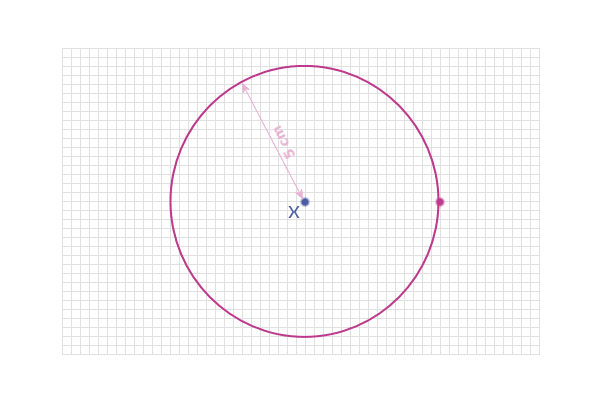
By now, you should realise that all of these POINTS WHICH
OBEY THE RULE lie along a circle (of radius 5 cm, centre X):
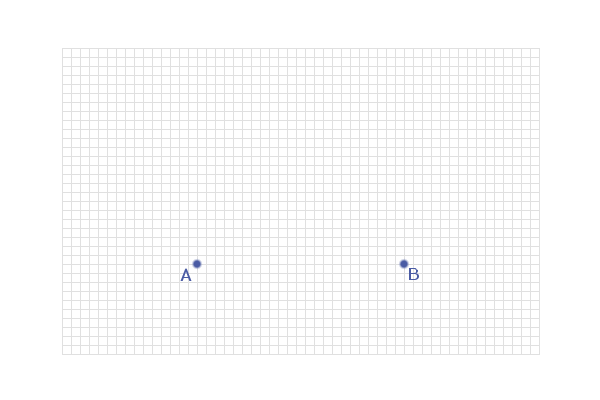
2. Equidistant from 2 points
e.g. Find the locus of points which are equidistant from the
points A and B in the diagram below
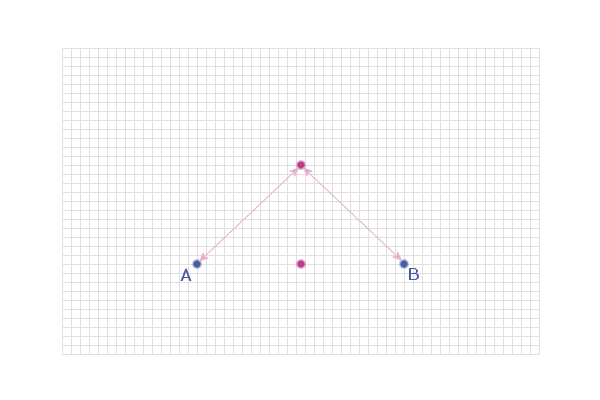
So, we want points that are an equal distance from A and from
B. The easiest point to locate first of all is the mid-point of
AB:
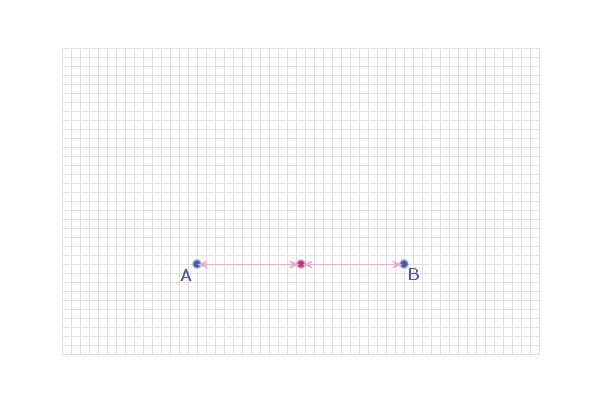
But, this point is also the same distance from A as it is
from B:
And, and point on this line is the same distance from A as it
is from B...
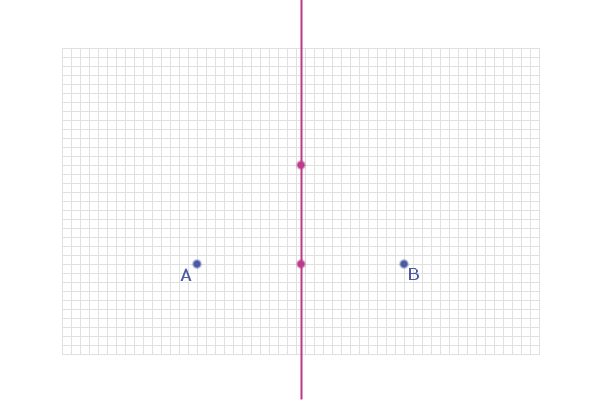
So, the locus of points that are equidistant from two fixed
points A and B is always the perpendicular bisector of AB...
3. Equidistant from 3 points
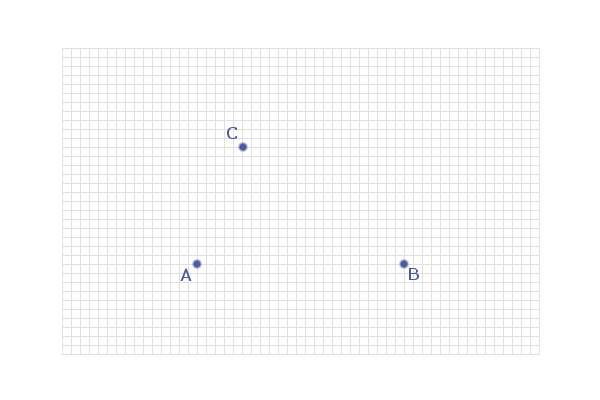
e.g. Find the locus of points which are equidistant from the
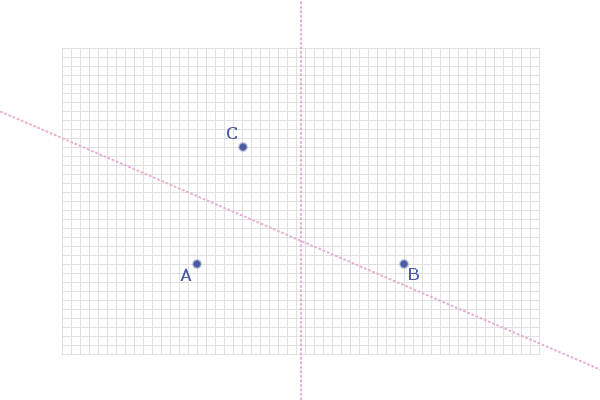
points A, B and C in the diagram below
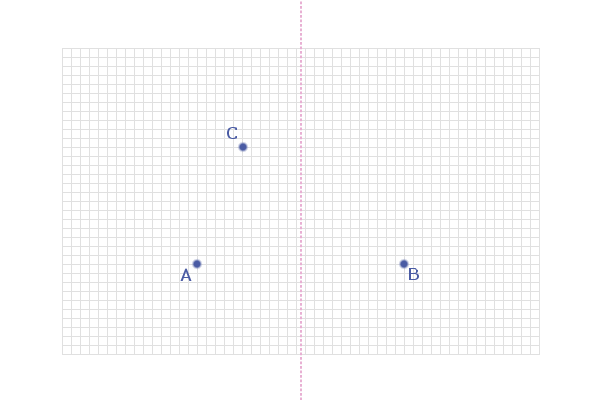
We already know that the points equidistant from A and B lie
on the perpendicular bisector of AB:
Similarly, the points equidistant from A and C will lie on
the perpendicular of AC (shown below):
Well, there is only 1 point that lies on BOTH of these lines
(and so is an equal distance from A, B and C):
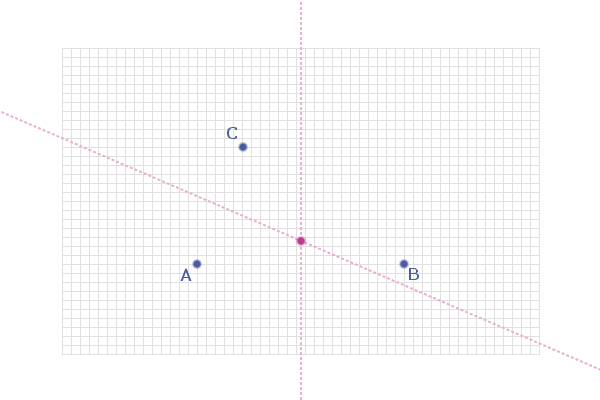
Note: The point is also the centre of the circle that passes
through A, B and C...
4. Equidistant from an infinite line
e.g. Find the locus of points which are 3 cm from the
infinite line shown in the diagram below
This point is 3 cm from the line:
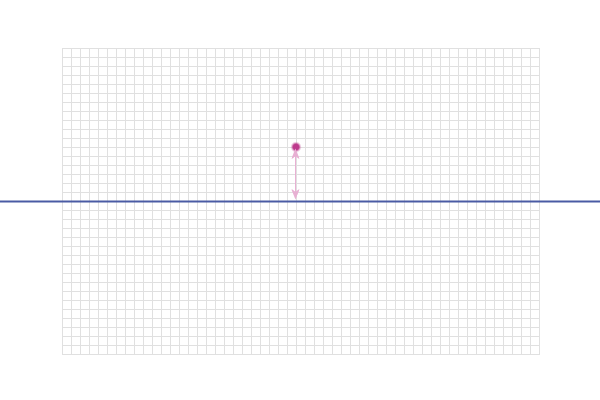
So is this point:
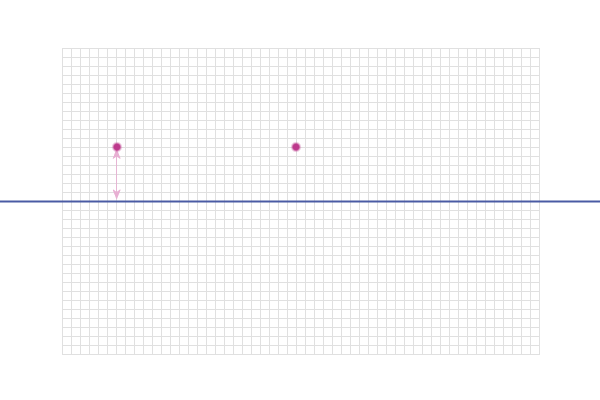
And this point:
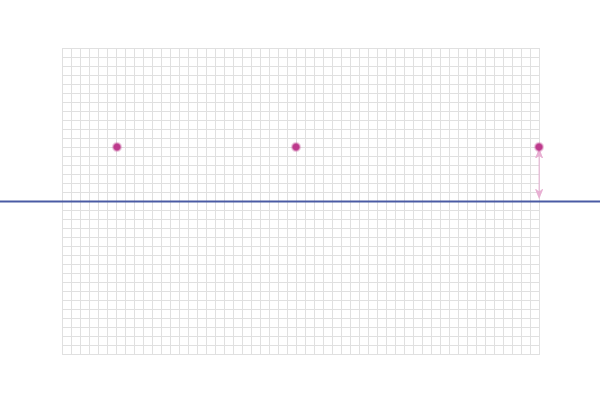
Connecting these together, we find all the points on this
line are 3 cm from the infinite line AB...
But also, this point 3 cm below the line is also 3 cm from
the line AB:
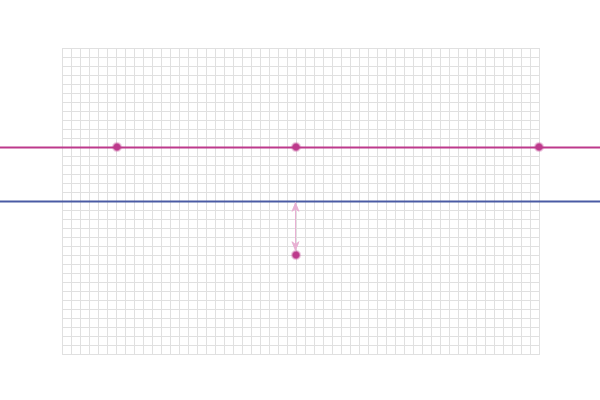
So, all the points on this line are also 3 cm from AB:
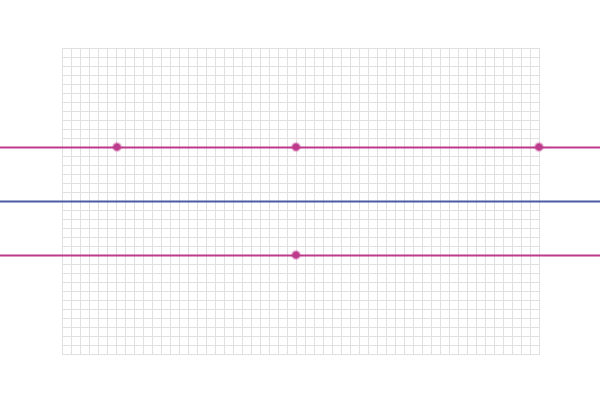
So, the locus of points 3 cm from the infinite line AB is 2
lines which are parallel to AB (one 3 cm above it and one 3 cm
below it)...
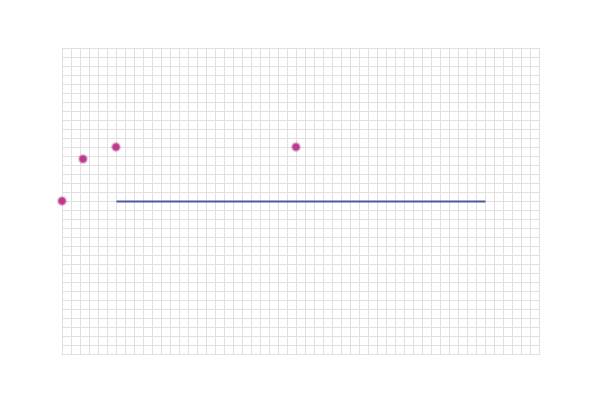
5. Equidistant from a finite line
e.g. Find the locus of points which are 3 cm from the finite
line AB shown below
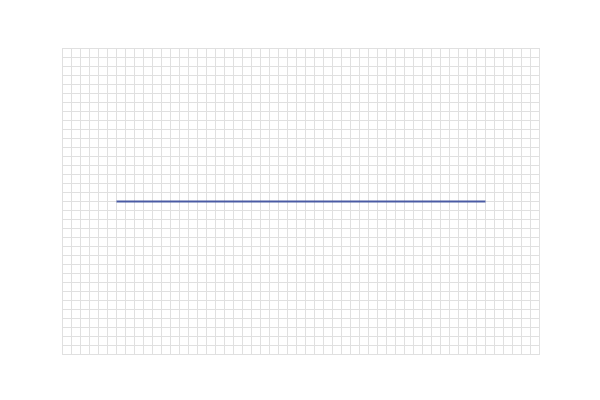
We start of just as we did in the previous example, finding a
point 3 cm above the line AB:
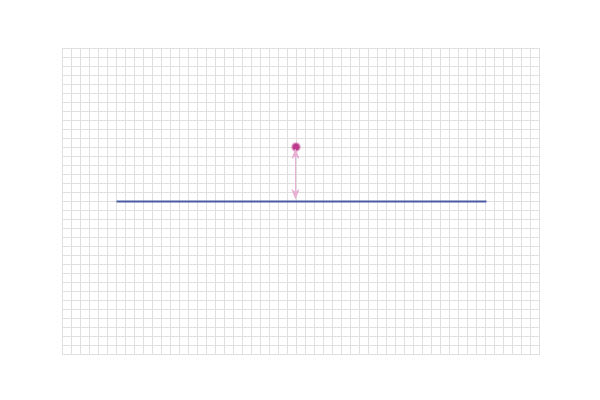
And then another point...
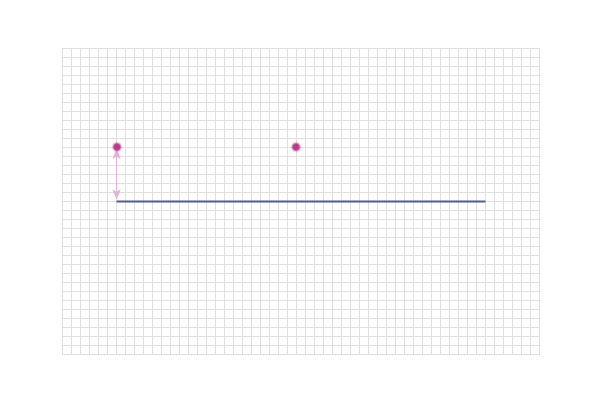
But a point that is 3cm from the end of the line might be
this one:
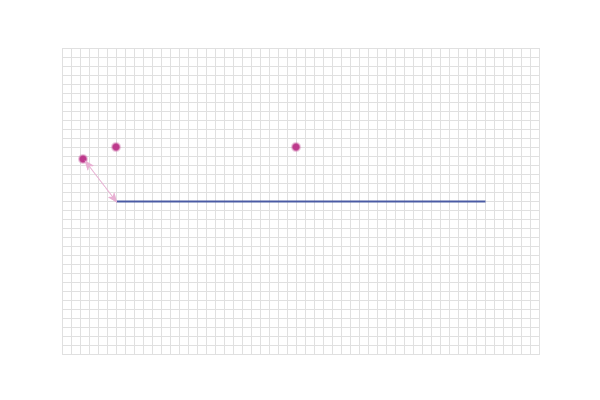
Or, it might be these...
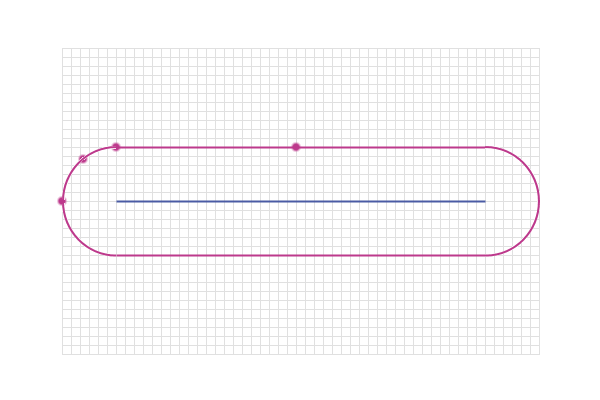
So, we end up with a semi-circle at each end - so the locus
looks a bit like a running track:
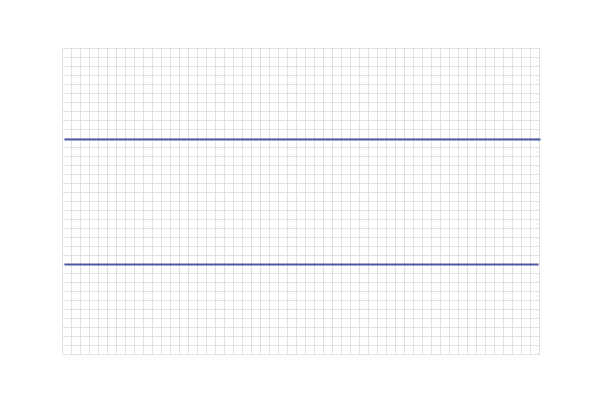
6. Equidistant from two (parallel)
lines
e.g. Find the locus of points which are equidistant from the
2 lines shown below
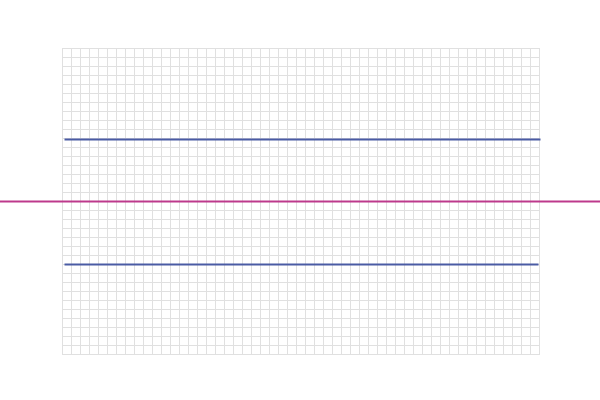
Quite easily, this is the points on the parallel line that is
halfway between them...
7. Equidistant from two (non-parallel)
lines
e.g. Find the locus of points which are equidistant from the
2 lines shown below
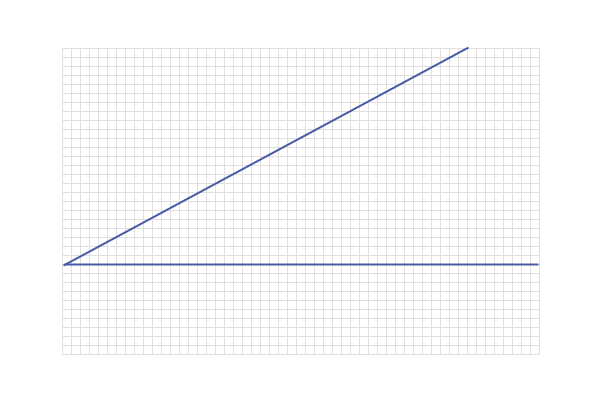
The point I had added in below (halfway along the vertical)
is WRONG!
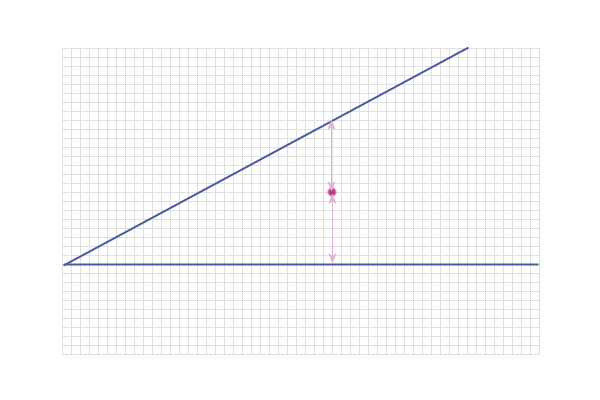
Because the distance from a point to a line is always
measured as the shortest (i.e. perpendicular) distance from the
point to the line - and you can see then that the correct point
is a bit below the incorrect one I used above:
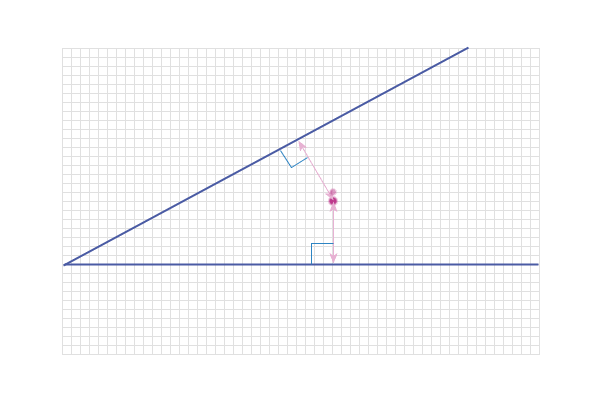
Here is another point that is correctly the same distance
from both lines...
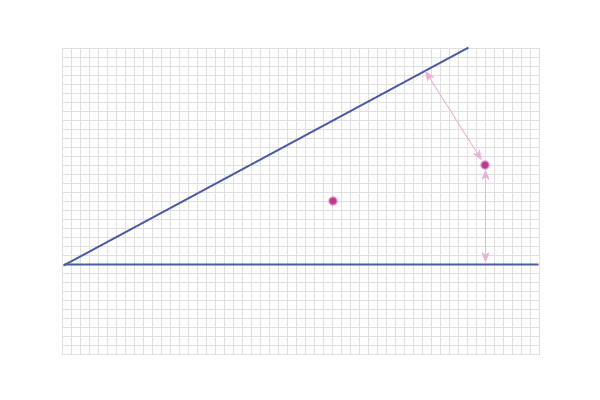
And in fact, all the points along this line are equidistant
from the two lines
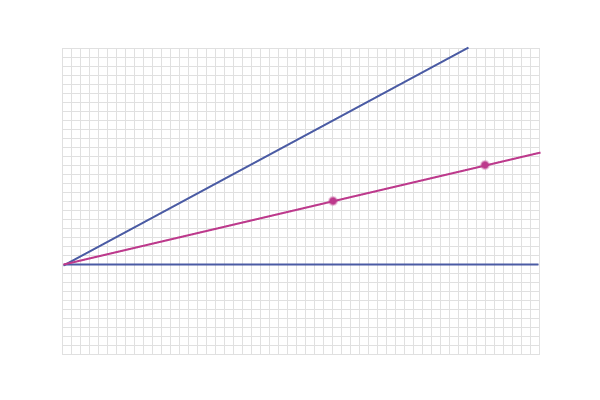
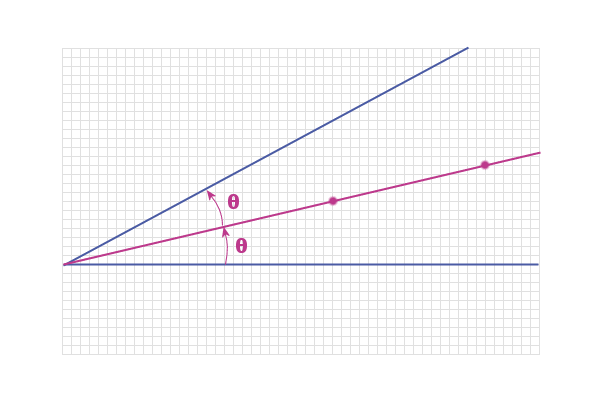
Note: This line is the bisector of the angle between the
lines:
8. Equiangle from a line (90°)
e.g. Find the locus of points X such that angle AXB is 90°
We've got to find a point (‘X’) such that the angle AXB
is 90°
Here's my first guess...
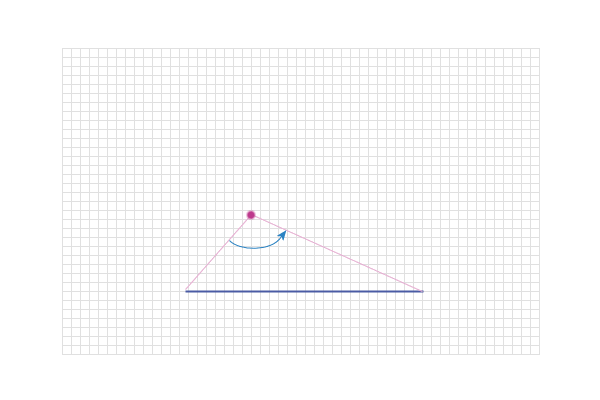
And clearly, the angle is too big on that one (above) - but
if I just move my point up a bit until the angle becomes 90°:
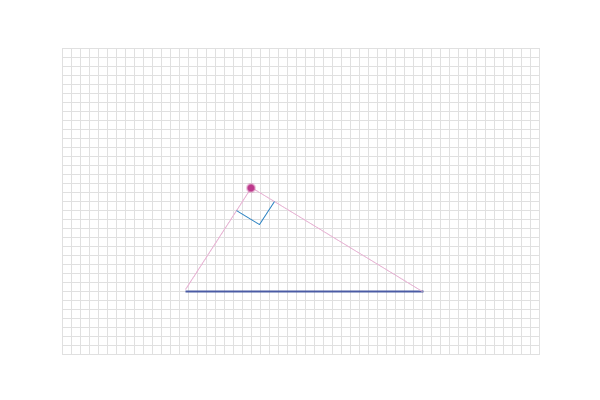
Here's another point, carefully located so that the angle is
90°
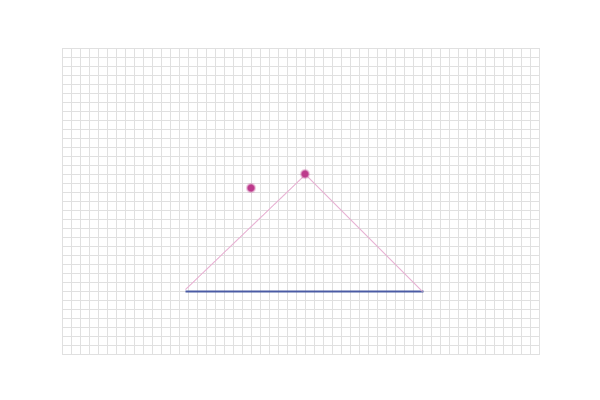
And another:
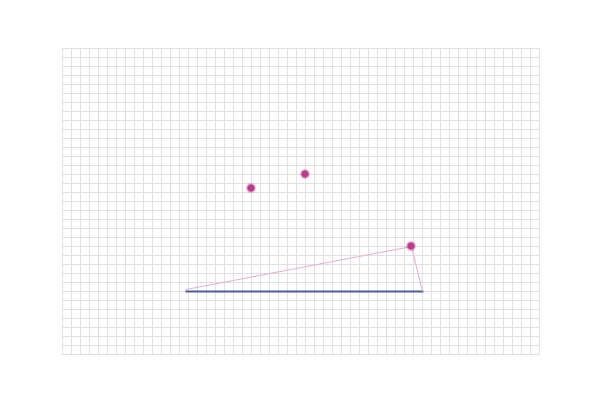
And, if we connect up all of these points, we get a circle
which has the mid-point of AB as its centre and AB as its
diameter:
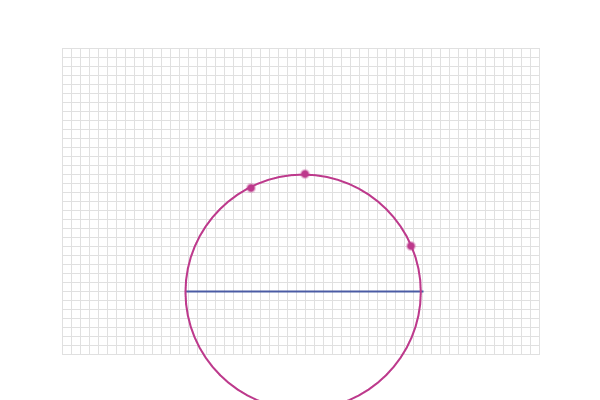
9. Equiangle from a line (not 90°)
e.g. Find the locus of points X such that angle AXB is 55°

Similar problem really - Carefully locating a point so the
angle is 55°:
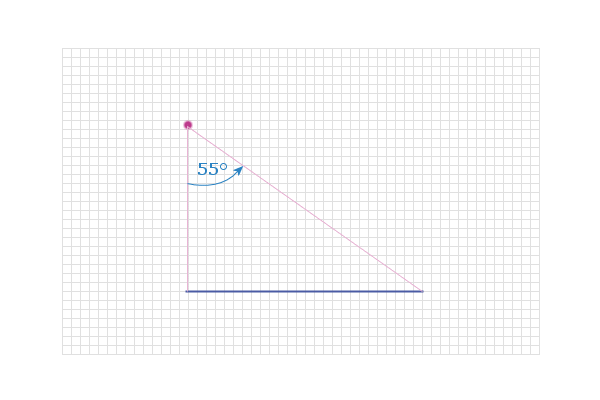
And another:
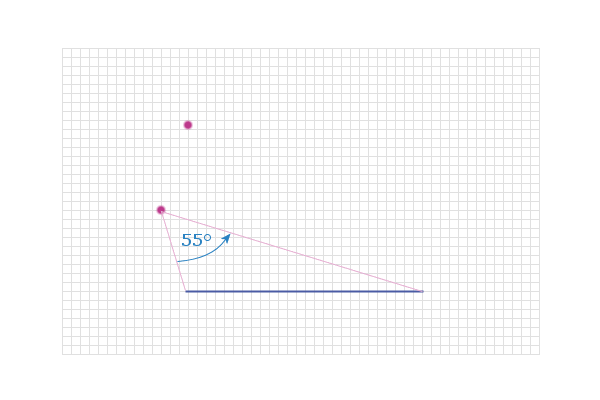
And another:
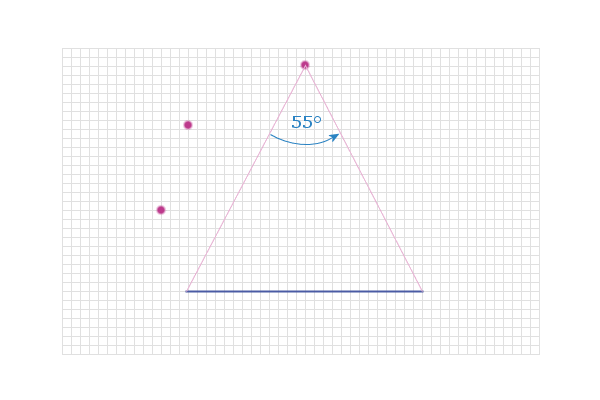
And connecting these points, we produce the arc of a sector
of a circle - this should remind you of the ‘angles from a
chord’ rule you learnt in ‘Circle Theorems’:
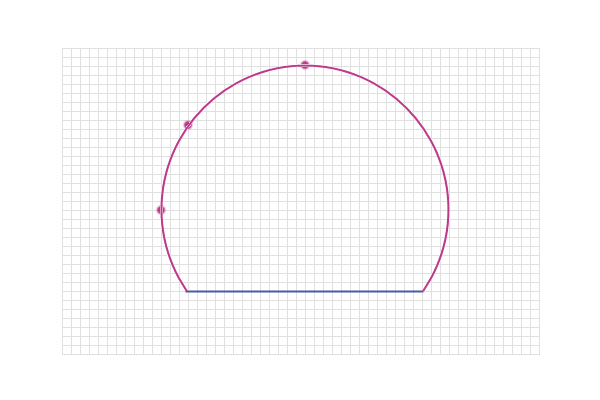
These are the standard results, but it is easy to create
completely wacky questions. If you know the standard results,
you'll be able to cope...
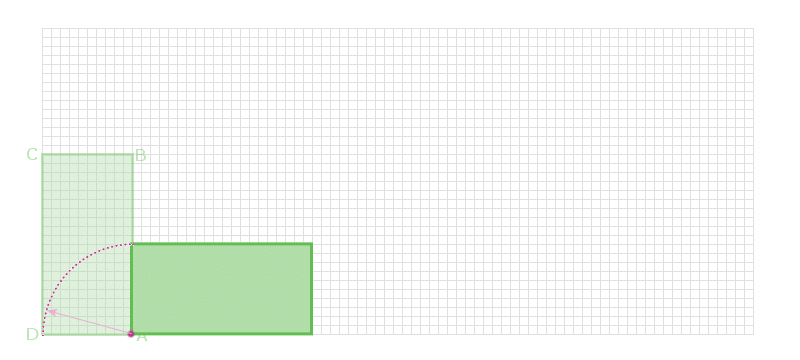
e.g. The parcel below is 'rolled' along the ground in this
way
First of all, it it tipped about the point A until the side
AB is on the ground. Then it is tipped about the point B until
the side BC is on the ground... Etc - until the the side AD is
on the ground again
Describe the locus of the point D

As the parcel rotates about A; so the line AD rotates and the
arc traced by the point D is shown:
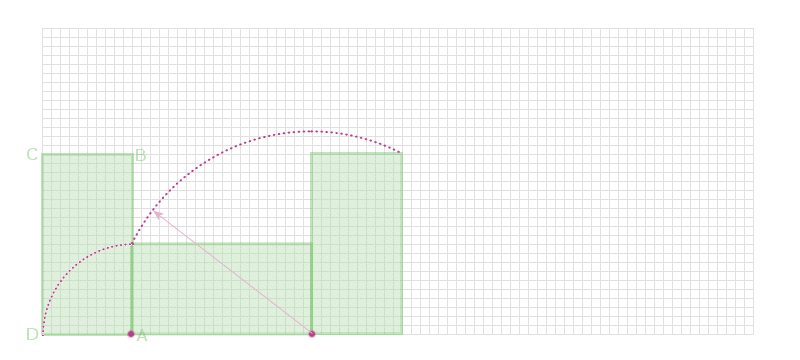
Now, the parcel rotates about B, so the arc formed has the
same length as BD (i.e. the diagonal of the rectangle):
And now the parcel rotates about 'C':
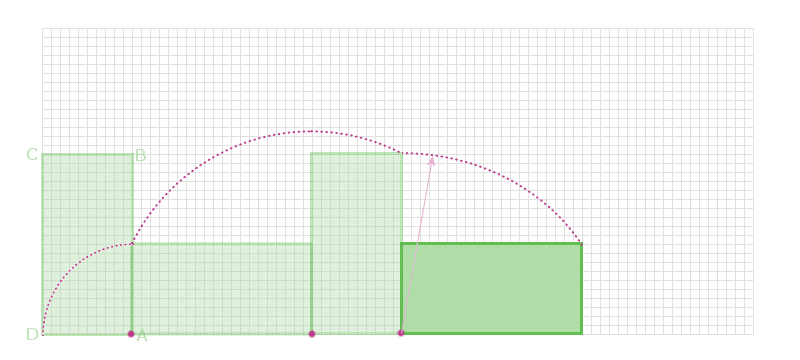
etc...
The dashed purple line shows the locus of the point 'D' as
the parcel is 'rolled' along the ground
Sorry - there are no hints for these
questions
Make sure your diagrams a clearly drawn and
properly constructed
(using compasses and rulers)
|
















































